This post is a follow-up to Sarah Stephens' guest post of a week ago, in which she described a lesson using embodied cognition to help students make sense of the interior angle sum theorem for triangles, not just as an abstract concept, but as a property grounded in their concrete physical experiences.
Category Archives: Geometry
The Interior Angle Sum: An Embodied Investigation
[This guest post by Sarah Stephens, a senior at Pennsylvania State University, describes a lesson she created as part of her Senior Honors Thesis on leveraging embodied cognition to help students develop abstract mathematical concepts.]
As a soon-to-be classroom mathematics teacher, I have taken special interest in the field of … Continue Reading ››
Protect the Sheep
A game of enclosing sheep and wolves in fences helps children to develop their conceptual understanding of polygons.
Constructing the Pi-Petal Rose
When I was introduced to radian measure in high school, I knew just one thing: How to convert between radians and degrees. Had you asked me to illustrate a radian on a circle or to explain why radian measure was useful, I would have been stumped.
In this post, I'll describe a Web Sketchpad activity … Continue Reading ››
Catching Up with New Web Sketchpad Functionality
This past January, we introduced the Web Sketchpad Tool Library and Viewer. The Tool Library is a collection of over 60 mathematical tools for customizing a Web Sketchpad model, making it possible for teachers to decide which tools students have available to them on an activity-by-activity basis. The Viewer is a site … Continue Reading ››
Circle Tracer Challenges
Geometry tends not to receive much love in elementary curricula, and that's a shame. In this post, I'll describe some of my new ideas for using Web Sketchpad to introduce young learners to fundamental properties of circles.
On page 1 of the websketch below (and here), begin by asking students to drag … Continue Reading ››
A Double Spiral from David Henderson
 David Henderson, the author of Experiencing Geometry, died this past December. I wrote about David in a prior post, and in particular, his approach of asking us to grapple with a small number of rich problems, allowing us to find our own, often non-traditional, ways of … Continue Reading ››
David Henderson, the author of Experiencing Geometry, died this past December. I wrote about David in a prior post, and in particular, his approach of asking us to grapple with a small number of rich problems, allowing us to find our own, often non-traditional, ways of … Continue Reading ››
The Perimeter Problem
At a recent meeting of mathematics content coaches (many from the organization Reimagined) we investigated the following problem: What is the perimeter of the polygon below?
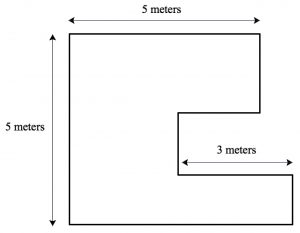
It appears at first that there isn't enough information to solve the problem. Indeed, the lengths of only three of the polygon's … Continue Reading ››
A Dynamic Approach to Finding Pirate Treasure
In his 1947 book, One, Two, Three...Infinity, physicist George Gamow poses a pirate treasure problem that has since become a classic. Below is my reworded statement of the puzzle.
Among a pirate's belongings you find the following note:
The island where I buried my treasure contains a single palm tree. Find the tree. From the palm tree, … Continue Reading ››
The Scaled Maps Problem
Below are two maps of the United Sates, with the smaller map a 50 percent scaled copy of the original. The edges of the two maps are parallel. Imagine that the maps are printed out, with one resting on top of the other.
Believe it or not, you can stick a pin straight through both maps … Continue Reading ››