Like other enthusiasts of mathematics, I’m captivated by the way that mathematical ideas can explain things in the physical world around me, and by the way that I can carry out mathematical thought experiments in my mind and then apply the results to control my external physical environment.

But it turns out that my separation of the two elements here—the internal activity of mathematical thinking and the external sensory-motor activity of perceiving and acting upon things in the outside world—is a bit naïve. Findings from cognitive science raise questions about the dichotomy and suggest ways in which thinking is inseparably integrated into our senses and our movements. As humans we think not only with our brains, but also with our hands, our voices, our eyes, ears, touch, and smell.

For me, this was one of the main themes of the ICME conference that I began to describe in my last blog post. At the Congress, Luis Radford from Laurentian University was presented with the organization’s Freudenthal Award. In his award lecture (download), he discussed students’ early algebraic thinking, and described a “theory of teaching and learning … that emphasizes the sensible, embodied, social, and material dimension of human thinking.” His description of thinking as having an embodied and material dimension, and the examples he gave from his work with students, help to clarify the idea that thinking integrates both mental and physical aspects, and as educators we can do a better job by paying close attention to the physical aspects of student thinking.

One example came from an activity in which 9^th graders were given the pattern of circles shown below and asked to formulate an algebraic expression to describe how many circles were in each term.

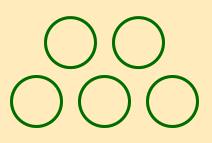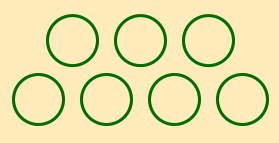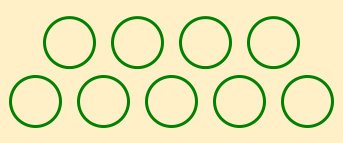First Term	Second Term	Third Term

The video of Mimi’s work showed her combining both voice and gestures in her thinking about the algebraic expression for the first term:

(pointing) “one,”	(pointing) “one,”	(looping) “plus three,”

Mimi’s initial conception of the expression consisted of pointing and looping gestures accompanied by words:

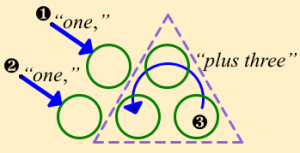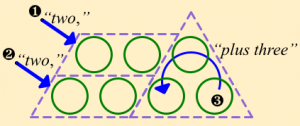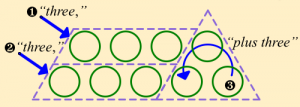Radford calls Mimi’s result an embodied expression because the three terms are represented by physical elements of gestures and words, rather than by symbolic variables. He goes on to describe how Mimi correctly answers a question about the tenth term by using the same embodied form of the expression: “(pointing) ten, (pointing) ten, (looping) plus three makes 23.”

I found this revealing: that a student’s thinking about a particular algebraic expression might initially represent the expression as an integrated sequence of gestures and words, and further that this physical, exterior form of thinking would allow her to apply the expression to a different starting numbers to find the number of circles in the tenth term. She’s doing all the operations of algebra, including substitution, but with a variable that’s a physical gesture-and-word combination. Radford observes that Mimi, and the other students in his study, were able to move “unproblematically from an embodied form of thinking to a symbolic one,” transforming “(pointing) one, “(pointing) one, (looping) plus three” into n + n + 3 (and subsequently into 2n + 3).

I hadn’t thought much about how such sensory-motor elements as Mimi’s pointing with her finger while saying “one” are not just physical actions, but are also an integral part of the thought process. We think with our hands, our voices, and our senses as well as with our brains.

In a way, I already knew this. When I struggle with an idea or a plan and clarify my thinking by explaining it to someone, it may not matter whether the person can respond in a meaningful way, or even understands what I’m talking about. In fact, I’m thinking with my voice, my gestures, my eyes, and my ears as I formulate and listen to my own explanation. My thinking process plays out, not only in my brain, but also in my sensory-motor system.

This aspect of human cognition is a powerful theoretical argument for the importance of manipulatives, of inquiry-based learning, and of software like Sketchpad, Fathom, and TinkerPlots that engage students’ minds through their sensory-motor systems.

This theme from ICME — the way in which we humans think with our bodies as well as our brains — stresses the connections between students’ mathematical concepts and the real-world objects that embody those concepts. Lakoff and Nuñez observe, in the introduction to their book Where Mathematics Comes From: How the Embodied Mind Brings Mathematics into Being:

“For the most part, human beings conceptualize abstract concepts in concrete terms, using ideas and modes of reasoning grounded in the sensory-motor system. The mechanism by which the abstract is comprehended in terms of the concrete is called conceptual metaphor.”

It seems to me this notion of conceptual metaphor fits the gestures and words employed by Mimi, as well as most constructions that Sketchpad users build and explore. It further seems to me that this notion can be useful in understanding the importance of real-world actions and constructions in students’ efforts to form abstract mathematical concepts.

Finally, these related thoughts, from Radford and from Lakoff and Nuñez, are already proving of value to me in describing the work that Daniel Scher and I have been doing on “geometric functions,” which was also the topic of the discussion group that I organized at ICME. I’ll describe that discussion group in my next post.