The title of this post is a nod to the Sketchpad activity module Pythagoras Plugged In by Dan Bennett. Dan’s book contains 18 visual, interactive proofs of the Pythagorean Theorem. And there are more:  The Pythagorean Proposition, published in 1928 by Elisha Scott Loomis, contains over 350 proofs, 255  of which are geometric. Wow!

I revisited the Pythagorean Theorem last month when preparing for a professional development summer institute hosted by Metamorphosis, a New York-based provider of content coaching. My colleagues Anne Burgunder, Shaun Porter, and I wanted to introduce our teachers to a visual proof of the theorem, but when we reviewed existing lessons, we notice that nearly all start by providing students with static illustrations of squares and triangles and then lead them through the steps to prove that the relevant areas are equal. Could we engineer the investigation so that the teachers could create illustrations of their own?

We posed the following two dissection tasks to the teachers without referencing the Pythagorean Theorem:

• Draw a square. Divide your square into two smaller squares and four congruent right triangles with nothing left over.
• Draw another square. Divide the square into one smaller square and four congruent right triangles with nothing left over.

We gave the teachers five minutes to sketch some possibilities on paper and then asked a few of them to share their work on the whiteboard. Here is what they drew:

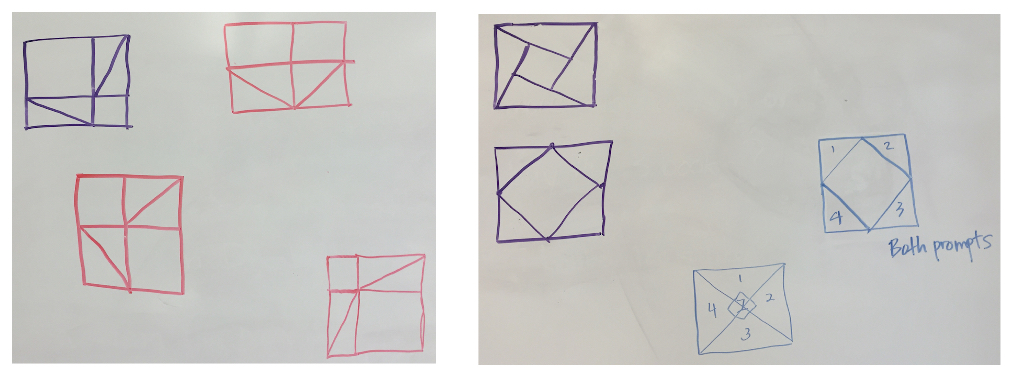
In surveying the drawings of the entire class, Shaun and I noticed that many participants added constraints to the task that did not appear in the instructions. In the picture below on the left, the two smaller are congruent and the right triangles are isosceles—conditions not required by the problem. And in the picture on the right, the vertices of the inscribed square sit at the midpoints of the outer square, again creating isosceles right triangles.

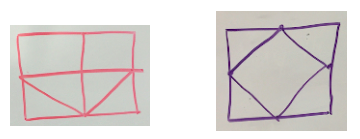
Undoubtedly it’s easier to focus on special cases then head straight for the most general illustration, so it did not seem surprising that our participants had favored this approach. Indeed, this was a perfect opportunity for us to introduce the role that dynamic geometry could play in the investigation: Rather than create static illustrations that were overly specific, we could use Web Sketchpad to create an interactive model showing the full range of solutions to the two drawing problems.

As we began the Web Sketchpad construction below (and here), we added some extra constraints to the original dissection challenge:

Draw two congruent squares. Divide the first square into two smaller squares and four congruent right triangles with nothing left over. Then divide the second square into one smaller square and four congruent right triangles with nothing left over. All eight of your right triangles should be congruent.

If you’d like to build your own interactive model of the picture below, you can use the websketch and accompanying how-to video at the end of this post.

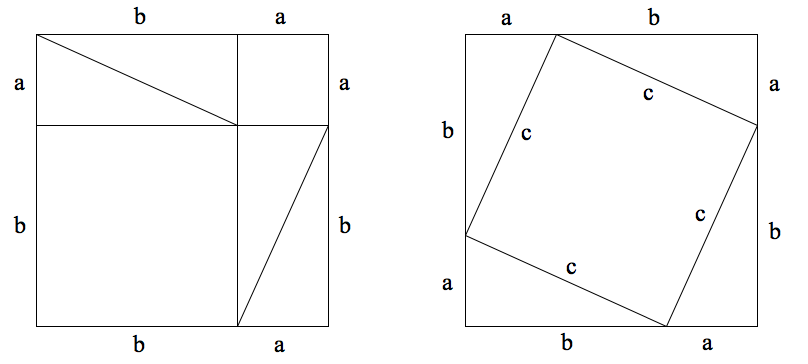
It was only after our teachers constructed this model  that we introduced the larger context of our investigation—the Pythagorean Theorem and its proof. Participants noticed that since the two overall squares were congruent as were all eight right triangles, we could conclude that the sum of the areas of the two smaller squares (a² and b²) was equal to the area of the  inscribed square (c²)—the Pythagorean Theorem!