I must admit that I am addicted to triangle shearing problems . I’ve written about them before, and will be revisiting them soon in my City College geometry class. I mention this because several weeks ago, I encountered a problem in the LinkedIn feed of mathematics educator James Tanton that made me wonder whether a shearing approach might work.

The problem, inspired by Brad Ballinger, is as follows:

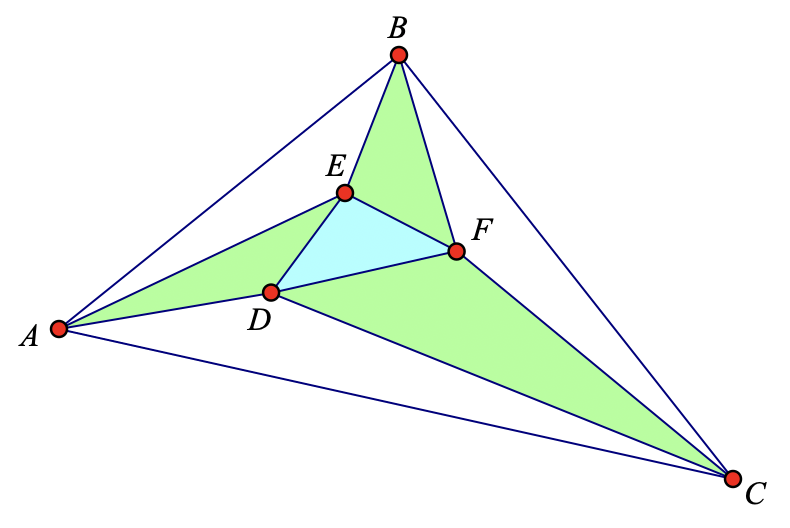
An arbitrary triangle DEF sits inside a larger arbitrary triangle, ABC. Show that the sum of the areas of the three green triangles is unchanged if you translate ∆DEF within the larger one. 

Tanton devised a proof of the result, but noted that it was complicated and challenged his readers to find a simpler proof. With no clear sense of whether shearing might help, I set out to shear the triangles, using Sketchpad as my construction tool. Soon enough, I had a very elegant solution in hand. Below (and here), I outline my approach. Use the page controls in the lower-right corner to move from page to page.

When I shared this result with Michael de Villiers, he soon discovered that the result holds not just for triangles, but for any two random polygons that share the same number of sides. In fact, the result is even more general in that the polygons need not be convex, and the inner quadrilateral can move outside, provided one uses directed areas.