When Scott Steketee and I developed activities for the Dynamic Number project, we thought about ways that dynamic array models could help children to conceptualize multiplication.

Rather than presenting children with arrays that were fully formed, we thought it would be instructive for them to build these arrays themselves. That design goal led to the following multi-level game in which students construct buildings from the ground up to model multiplication with arrays.

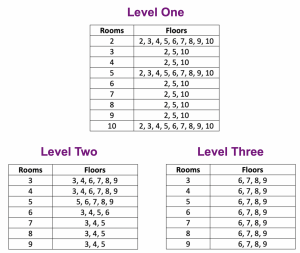
There are three levels to the game (below and here), each on its own page.  The goal of the game is to construct a building based on the given specifications and then determine how many total rooms the building contains. The building starts as a single room, but by dragging the two handles attached to the room, you can change the number of rooms per floor by dragging horizontally and the number of floors by dragging vertically. There are 10 problems per game, with a maximum score of 100 points. Missing a problem and trying again reduces the value of a correct answer by 2 points. Problems are presented randomly in each level, with level one focusing on multiples of 2, 5, and 10 and levels two and three progressing to other multiples. The tables at the end of this post list the possible problems for each level.

Here are some of the ways that students might interact with the model and use it to develop a deeper sense of multiplication:

• We constructed buildings and counted each room one by one to find the total.
• In a building with 4 rooms on each of 7 floors, we added 4 + 4 + 4 + 4 + 4 + 4 + 4 = 28.
• We skip counted by the number of rooms per floor to find the total.
• We skip counted, too, but we skip counted by the number of floors if it was an easier number. For example, when there were 7 rooms on 5 floors, we skip counted by 5s seven times to get 35 rooms because it was easier than skip counting by 7s five times.
• We looked for multiplication facts we knew. For example, we constructed a building with 6 rooms on each of 8 floors. We knew 5 rooms on 8 floors is 8 × 5 = 40, and then we added the 8 rooms in the last column to get 48.
• We thought of large buildings as a collection of smaller buildings. We found the total number of rooms in each of the smaller buildings and then added them together. For example, for a building 8 floors high with 4 rooms on each floor, we broke it into two smaller buildings of 4 floors each with 4 rooms per floor. We found 4 × 4 = 16 twice to get 16 + 16 = 32.

The Construct a  Building activity served as a first step in the creation of what would eventually become Bunny Times  —another array-based multiplication game with charming graphics and added  support for deconstructing problems like 7 x 8 into (5 x 8) + (2 x 8).