Welcome back to my ongoing series in which I feature interactive Web Sketchpad models that draw conic sections. Today’s installment, like the previous one, focuses on ellipses, and dates back to the 17th-century Dutch mathematician, Frans van Schooten.

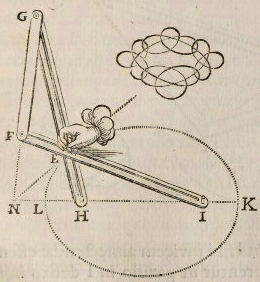
Below is an image from van Schooten’s manuscript, Sive de Organica Conicarum Sectionum in Plano Descriptione, Tractatus (A Treatise on Devices for Drawing Conic Sections). The obvious level of care lavished on the illustration is consistent with all the drawings in van Schooten’s work.

Van Schooten’s linkage consists of three moveable rods hinged together. The model is built so that HI = FG and IF = GH.

The interactive Web Sketchpad model below allows you to experiment with van Schooten’s linkage. Drag point F and observe the trace of point E. Press Animate Point F to see the linkage move on its own and press Show/Hide Locus to see the curve traced by point F all at once. You can change the lengths of the rods by dragging the red points at the bottom left.

It certainly appears that point E traces an ellipse, but can you prove it? The proof is not hard and is a great opportunity for students to apply what they know about triangle congruence. Press Proof Hints for step-by-step guidance.

You’ll find a desktop Sketchpad model of the congruent triangle construction as well as accompanying teacher notes and a student worksheet in my book, Exploring Conic Sections with The Geometer’s Sketchpad.