A quick quiz: How many fractions are there?

This may sound like an absurd question, but in the context of elementary mathematics curricula, it makes a lot of sense. Think about it: Children encounter fractions like 1/2, 3/4, and 2/6 all the time, but do they ever see 1/100, 31/90, or 499/500? Unlikely. No brave soul will attempt to draw 3/100 on a whiteboard, and adding together fractions like 13/37 and 46/93 is unappealing at best.

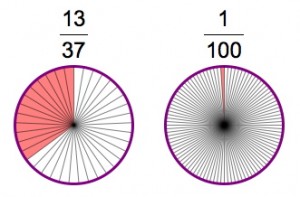
So when it comes down to it, children encounter relatively few fractions. If children’s exposure to integers were limited to those values between 0 and 100, we’d be aghast, but in the case of fractions, we’re content to focus on a paltry set of permissible values.

The NSF-sponsored Dynamic Number project at KCP Technologies (the sister company of Key Curriculum Press) is creating Sketchpad activities for grades 2–8 that focus on number, operation, and early algebra. My colleague Scott Steketee and I are heading the development work, and naturally we’re making interactive models of fractions.

In several of our activities, we provide students with area models of fractions in which they can change the numerator or denominator of a fraction and immediately view its corresponding picture, represented as shaded parts of one or more circles.

Children, mind you, know nothing about the rule among curriculum developers that the numerators and denominators of fractions must be chosen carefully. Indeed, we tried in vain to guide children in our field-test classrooms to experiment with “nice” values like 1/2 and 3/4, but they would have none of it. “Try a denominator of 100!” they’d shout.

With some trepidation, we entered 100. Because the model was built with Sketchpad, it had no problem displaying 1/100. Indeed, it could handily show a multitude of values. 13/37? Check. 499/500? Check. The children loved it.

After some initial play time with the fractions, we ask students to think about the following question: As the denominator of a fraction increases, does the fraction get larger or smaller? After experimenting with this Web Sketchpad model, they have no problem answering the question and can remember the reason why by recalling the sequence of fractions they viewed.

Can you think of other good uses for our Sketchpad fraction models? We’d love to hear your ideas!