Not long ago, I conducted a Saturday morning PD session for some Texas teachers participating in an NSF research project.
(The research is a controlled study of the relationship between students’ use of Sketchpad and their conjecturing and proving behavior. I hope we’ll have a blog post about this study itself before too long.)
Because of the emphasis of the project, I wanted to use an activity that focused on conjecturing and proving behaviors. These are high-level cognitive behaviors, behaviors that are required by tasks with a high level of cognitive demand.
Scaffolding an activity appropriately to create and maintain high cognitive demand is critical, but hard to do. This might be described as the Goldilocks problem: too much scaffolding takes away the challenge, too little leaves students floundering, so we need just the right amount of scaffolding. But our problem as teachers is harder than the Goldilocks problem, because “just right” scaffolding is different for different students.
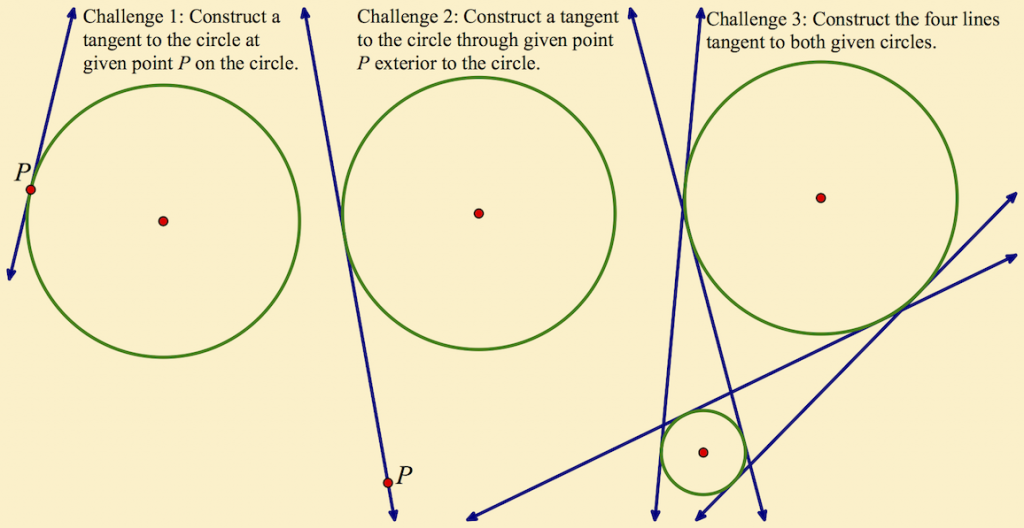
I began our session with a warm-up in which I used three related challenges, with each leading to the next (and with varying cognitive demand):
After some time, we discussed the warm-up. I then passed out four versions of another activity in which students investigate the relationships between angles and arcs in a circle. All four versions (available here) ask students to construct and investigate, and then form and prove conjectures, but they provide different levels of scaffolding, with each successive version at a higher level of cognitive demand.
I asked the teachers, working in pairs, to first review all four versions of the activity, and then to choose a version that seemed “just right”—challenging but not overwhelmingly difficult. Teachers then worked on their chosen version of the activity, and were free to consult the other versions of the activity if they got stuck and felt the need for more scaffolding.
We finished with a discussion of how teachers had chosen the version they did, and how they thought an activity like this would work in their own classrooms. Was the range of scaffolding wide enough? How can they encourage students to choose the most challenging formulation of the activity, but still within their reach? How can an activity like this encourage student persistence, while still allowing them to drop back a level (for more scaffolding) when they’re truly spinning their wheels?
Though we had a good exchange, we’d have needed far more time than we had that morning to give these questions the full examination they demand.
For me personally, the session was a good chance to think and strategize about the perennial Goldilocks problem with creating Sketchpad activities for others to use: How much scaffolding is appropriate? If there’s too little, the activity becomes inaccessible to Sketchpad beginners. But if there’s too much, experienced students may take the easy way out and follow step-by-step instructions rather than thinking more deeply about how to accomplish the mathematical goal.
I’d love to know what you think. How do you approach differentiation in your students’ use of Sketchpad, and how do you engage your students in Sketchpad activities that are more and more intellectually challenging as their Sketchpad skills and mathematical knowledge grow? Do the four versions of the same activity that I used seem like a useful model? How would you improve such a model?
(The Mathematical Task Framework for categorizing cognitive demand is described in Implementing Standards-Based Mathematics Instruction by Stein et. al. Henningsen and Stein describe how to maintain high-level thinking during actual classroom use in their chapter “Supporting Students’ High-Level Thinking, Reasoning, And Communication In Mathematics” in NCTM’s Lessons Learned from Research.)
re: Challenge 2 – My first thought was to approach this backwards from the way you do. Instead of starting with a line through point P, start with the tangent line at point T and then move T, and the tangent line, around the circle until the line intersects point P.
Hi Henry,
Your description actually sounds more like the easier Challenge #1, unless I’m misreading your comment. If I understand your approach correctly, here’s the problem: how do you determine where to put point T so that the line really does go through P? A visual determination is inexact; Euclid would be displeased, and a measurement of the distance between point P and the tangent line will always be non-zero (though you could make it very small, of course).
It may be that the hint I give at the end of the movie is a bit too opaque; I was concerned about giving away too much information for what I found to be a very enjoyable challenge. I’ve just put up a post on Sketch Exchange that gives more detail about the hint — about how to use the information you know to create a pattern that is very revealing. My sketch exchange hint is here:
http://sketchexchange.keypress.com/forum/showthread.php?105-Constructing-an-accurate-tangent-line-along-the-exterior-of-a-circle
Αγαπητέ κύριε,
Σας πληροφορώ ότι,στην προσπάθειά μου να επιλύσω κάποιο πρόβλημα διαπύστωσα ότι δεν μου δείνει σωστά αποτελέσματα.Διαπυστωστε και μονος σας οτι αν σχηματίσω δύο γωνίες με καθετες πλευρές και πάρω την διαφορά αυτών θα έπρεπε να μου δίνει αποτελεσμα 0.Τούτο δεν συμβαίνει.
Με τιμή Ανάργυρος Μαστρογιάννης
We’re lucky to have a Greek speaker on staff, but we’re still not entirely sure what you’re saying other than you get a different result. Is it possible for you to write your comment in English?