Shiva Gol Tabaghi obtained her PhD degree in Mathematics Education from Simon Fraser University in 2012. This guest post is based on her doctoral dissertation research. Presently, she is involved in teaching undergraduate mathematics courses at Simon Fraser University. She enjoys using dynamic geometric diagrams to influence students’ ways of thinking about mathematical concepts.

If you’ve taken linear algebra, chances are your introduction to eigenvectors and eigenvalues was not based on a geometric interpretation of these concepts. Indeed, when I reviewed a sample of linear algebra textbooks, I found a procedural algebraic approach to be dominant.

Recall that the algebraic method begins by finding eigenvalues (the roots of the characteristic equation det(A – λI) = 0) and then finding the associated eigenvectors (the non-trivial solutions for (A – λI)x = 0 given λ). If x is an eigenvector of A, then Ax = λx.

The algebraic method does not reveal the connections between linear transformations, eigenvectors, and eigenvectors. In fact, it hides the fundamental property that an eigenvector is a special vector that is transformed into its scalar multiple under a given matrix of transformation.

My findings motivated me to design a Web Sketchpad model that allows students to explore eigenvectors and eigenvalues from a geometric perspective. In the interactive model below, A is a 2 x 2 matrix and x is a vector. You can drag x and view its effect on Ax. You can experiment with different matrices by entering new values for the four numbers that comprise A.

Here are a few exploration ideas to try with your students:

• Drag x in a circular path and explain how x and Ax behave. Do they ever overlap?  Do they become perpendicular? How do you know when you’ve found an eigenvector of A?

• Change the entries of the matrix to match the matrix below. Drag x to find places where x overlaps Ax. Then, find a place where the vectors are collinear but point in opposite directions. Estimate the ratio of the lengths of Ax and x. Press Show Matrix Calculations and drag the point labeled λ so that its value is equal to this ratio. How can you tell by looking at the value of det(A – λI) whether you’ve found the precise eigenvalue? If necessary, adjust λ so that it is an eigenvalue. Then, if necessary, adjust x so that x represents, as precisely as possible, the associated eigenvector. How can the value of (A – λI)x help you?

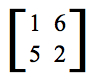
• Change the entries of matrix A to create a matrix that has eigenvalues of λ = 2 and λ = 4. Find the associated eigenvectors. How many of them can you find?

• Change the entries of the matrix  to the identity matrix. Drag x to find the eigenvectors of A. Explain your findings.

My students who interacted with this interactive model derived the following benefits:

1.  They overcame their difficulties in interpreting the equality sign in Ax = λx by visualizing the collinearity of Ax with x (for specific vectors x).
2. They developed an awareness of the existence of infinitely many eigenvectors, a fact that is hidden in the algebraic procedure for finding eigenvectors of a square matrix based on finding the eigenvalues first.
3. They explored the geometric representation of eigenvectors associated with negative eigenvalues. In the process, they developed a broader interpretation of the collinearity of vectors; that is, two vectors can be collinear but point in opposite directions.

I’d be interested to hear what your students discover when they try my interactive Web Sketchpad model. You can also download the desktop Sketchpad model, Eigenvectors.gsp.