Euclid’s Proposition 1 is notable for both its elegance and apparent simplicity. To construct an equilateral triangle from a given line segment, we need just two strategically placed circles to define its third vertex. Below is Oliver Byrne’s colorful take on the proposition from 1847.
How might we introduce this proposition to students if our goal is for them to use straightedge-and-compass tools, whether physical, virtual, or both, to build their own equilateral triangles? Exploring Geometry with The Geometer’s Sketchpad offers one possibility: give students step-by-step construction directions and then ask them to explain the reasoning behind the steps.
Another possibility, shown below (and here) with Web Sketchpad, is to provide students a Compass tool and a generic Triangle tool and challenge them to devise the construction method themselves (The video at the end of this post demonstrates the construction as well as the other investigations described here.)
But perhaps this is too big a leap. Might there be an intermediate step that doesn’t give away too much? Well, we could ask students to begin with the related task of constructing an isosceles triangle. Logically, this approach makes sense, but I’ve often wondered whether constructing one or even several isosceles triangles really gives students enough practice and insight into the role that circles can play in building equal-length segments. Without belaboring the point and asking students to construct a multitude of isosceles triangles, is there a context where building multiple equal-length segments feels engaging and worthwhile?
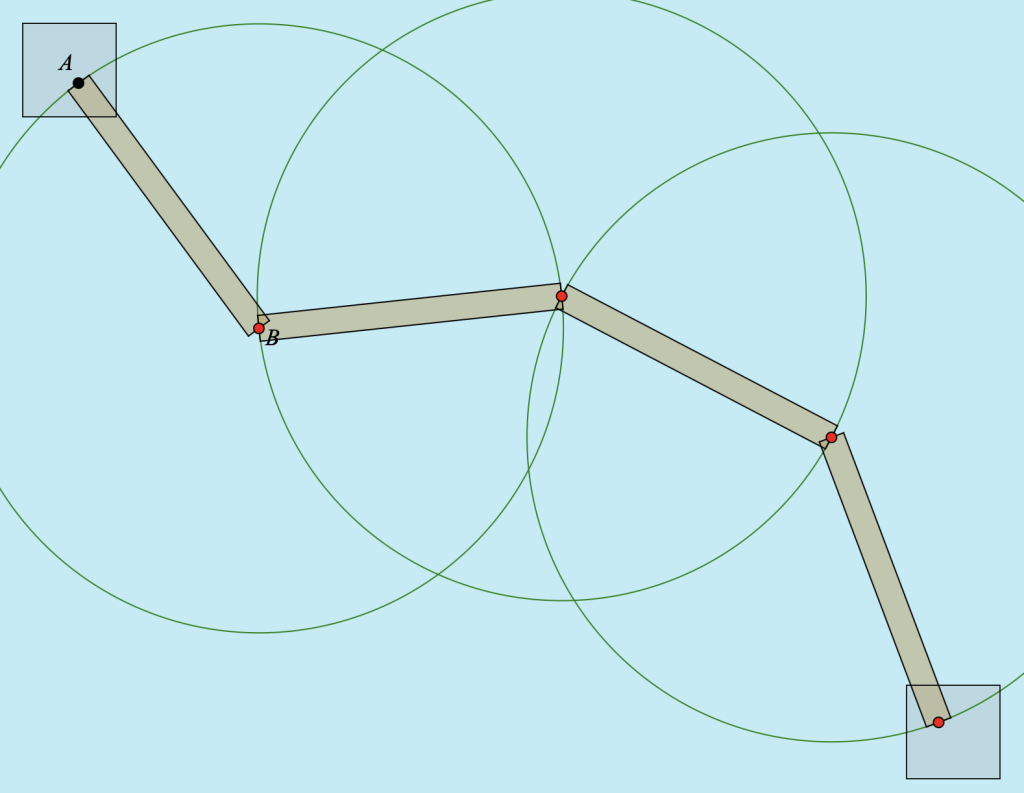
Page 2 of the webksketch above is my attempt at creating a suitable context. There are two square parcels of land, one in the top-left corner and the other in the bottom right. A wooden plank extends from point A into the water. Students’ goal is to create a boardwalk of planks, all of equal length, that connects the two plots of land. To construct the planks, students use two tools: the Compass tool and the beige plank tool.
As shown below, constructing circles, all with a radius equal to AB, is the key to the problem (The video demonstrates the construction.) Students can check their work by dragging point B and noticing whether all the planks remain equal in length. Making AB shorter may require adding more planks to the boardwalk.
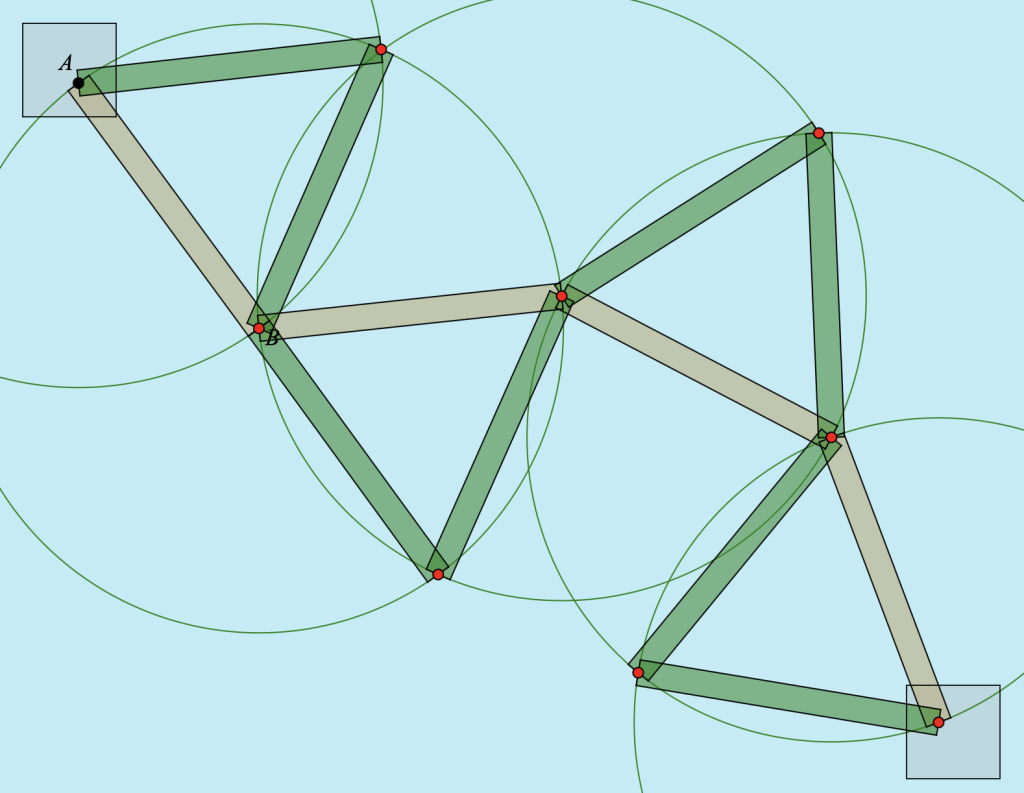
When I devised this scenario, I thought that its only connection to equilateral triangles would be to give students practice in creating equal-length segments. But that’s not the entire story: Having constructed the beige boardwalk, suppose we now wish to build a green boardwalk path connecting the same start and end points. We don’t want to walk on any of the existing planks, although it’s fine if our new path makes use of the existing spots where adjoining beige planks meet. Can we build the new path by constructing just two additional circles?
The picture below shows the surprising result: Four equilateral triangles composed of beige and green sides. This certainly wasn’t my goal when designing this activity, but what a nice outcome!