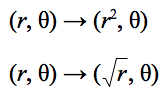Did you know that The Geometer’s Sketchpad is a great tool for creating funhouse mirror pictures? Sure, Sketchpad can reflect, rotate, translate, or dilate a picture, but these operations are rather tame: They transform images uniformly, producing pictures that are easily recognizable versions of the original. By contrast, Sketchpad’s “custom transform” feature allows you to apply non-linear transformations to pictures, resulting in images that distort the original in surprising, amusing, and instructive ways.

Last year, my colleague Scott Steketee wrote a blog post demonstrating the result of applying a sine function transformation to a picture of the Golden Gate Bridge. This transformation leaves the bridge in an a decidedly unsafe state for motorists and pedestrians!

I recalled Scott’s sine transformation while reading the just-released book, Math Bytes, by Tim Chartier.

Chartier devotes a section of Math Bytes to the visual effects of applying two polar coordinate transformations. Each transformation begins with a point (r, θ) and then either squares or takes the square root of r to obtain the transformed point:

When I read about these two polar transformations, I knew that I had to try them with Sketchpad. I began with the first transformation, taking a random point, calculating its
(r, θ) value, and then plotting (r², θ). With just these two points, I could teach Sketchpad (using its “custom transform” feature) how to apply this squaring rule to any point—or pixel—in the plane. Having done so, I selected a picture, choose my squaring transformation, and instantly moved each pixel in the picture to its new location.

You can download my Sketchpad file to see what I’ve done. In the sketch, I give an example of applying each of the two polar transformations to a picture, and explain how you can easily swap the picture with any image of your choosing. (Warning: If you experiment with photos of your friends and relatives, they likely will not find the results  flattering. It pays to distort your own face as well.)

To whet your appetite for experimenting, I’ve used the sketch to apply the polar transformations to six famous individuals and displayed the results below. How many can you recognize?