Arranging Addends is an interactive puzzle that I designed on a long bus ride through Alaska. The goal of the puzzle is to arrange the circles and the six numbers (1, 2, 4, 8, 16, and 32) so that three conditions are met simultaneously: The sum of the numbers in the green circle is 21, the sum of the numbers in the blue circle is 26, and the sum of the numbers in the red circle is 14. The numbers can be dragged into the circles, and the circles can be moved as well. Dragging the point that sits on the circumference of each circle changes the circle’s size.

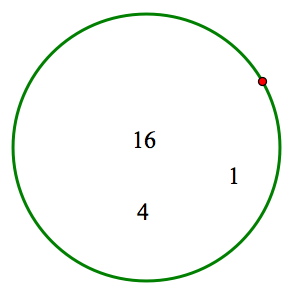
Students find it straightforward to satisfy the first condition of the puzzle. Dragging 1, 4, and 16 into the green circle fills it with numbers whose sum is 21. Creating simultaneously a sum of 26 in the blue circle is more puzzling. The only way to form 26 is to add 2, 8, and 16, but the 16 already resides in the green circle. How can it perform double duty?

Most students, after pondering this dilemma for a minute or two, have an “aha!” moment: What if the green and blue circles overlap each other, with the 16 sitting in their intersection? The picture below shows how this looks.

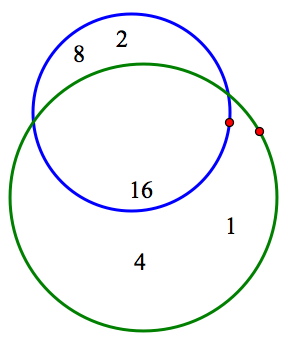
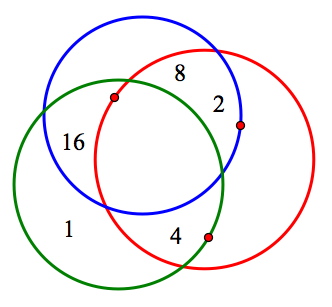Now, all that remains is to satisfy the final condition of the problem by making the numbers in the red circle sum to 14.  The only way to form 14 is to add 2, 4, and 8. But the way those three numbers are currently arranged makes it impossible to enclose them without including the 16 as well. Students soon realize that they need to adjust the numbers and circles to allow the 2, 4, and 8 to sit alone in the red circle while still keeping the first two conditions true (green = 21, blue = 26). The picture at right shows the final result, with all three conditions of the puzzle met simultaneously.

I’m especially pleased with the way the Arranging Addends puzzles require young learners to juggle and process multiple pieces of information. More often than not, the placement of the circles and numbers must be adjusted one or more times to ensure that the sum of each set of numbers matches the required value.

And the mathematics of the Arranging Addends puzzles runs deep. Each new challenge generated randomly by Sketchpad uses the same six numbers—1, 2, 4, 8, 16, and 32—as the elements for the three sums. These powers of two can, amazingly, form any sum from 1 to 63.

You and your students can play the Arranging Addends puzzles directly on this webpage using the interactive model at the beginning of this post. To obtain new challenges, simply press New Puzzle. You might also be interested in a low-tech version of the Arranging Addends Puzzles that requires nothing more than three hula hoops and a few pieces of paper. Regardless of which version you use, these puzzles are a great way to give your students practice in addition while keeping the work varied, interesting, and challenging.

You can play some variations of Arranging Addends here.