In my prior blog posts, I’ve described how to construct ellipses using linkages, concentric circles, congruent triangles, and tangent circles. These are all great methods, but I think I got ahead of myself: There’s a simple ellipse construction technique described in nearly every precalculus book that I’ve bypassed in my excitement to show you the more exotic approaches. Say hello to the pins-and-string technique:

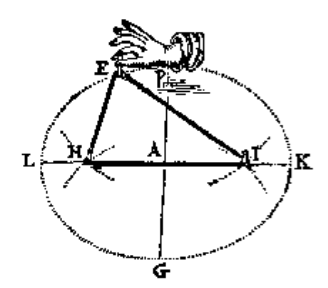The picture above comes from the 17th-century manuscript Sive de Organica Conicarum Sectionum in Plano Descriptione, Tractatus (A Treatise on Devices for Drawing Conic Sections)  by the Dutch mathematician Frans van Schooten. The ellipse construction in the illustration is quite simple. Press two pins into a corkboard, place a loop of string around the pins, pull the string tight with a pencil, and trace the pencil tip’s path as you pull the pencil around the taut string. Guaranteeing that the traced path is an ellipse is this definition of an ellipse: An ellipse is the set of points P such that PF₁ + PF₂ is constant for two fixed points, F₁ and F₂.

I don’t think any introduction to ellipses is complete without students making their own physical model of the pins-and-string construction and experimenting with how the distance between F₁ and F₂ as well as the length of the string affects the shape of the ellipse. But I also think there is value in building a Sketchpad version of the ellipse construction. Below is a pre-built Web Sketchpad model that your students can investigate. In my upcoming post, I’ll show how you can construct this model from scratch using Web Sketchpad.

You’ll find this construction, as well as many others, in my book Exploring Conic Sections with The Geometer’s Sketchpad.