As a student, I didn’t place conic sections on my list of favorite high school topics. The standard textbook treatment of the ellipse, parabola, and hyperbola seemed uninspired. There were messy algebraic equations with multiple square roots. There was lots of terminology. Drawing a conic meant plotting several points on graph paper and connecting them with a wobbly curve.
 I gave little thought to conics until I met David Dennis, then a fellow graduate student in mathematics education at Cornell University.
I gave little thought to conics until I met David Dennis, then a fellow graduate student in mathematics education at Cornell University.
David had a keen interest in the origins of curve-drawing devices. One historical figure in particular intrigued him: Frans van Schooten (1615–1660), a Dutch mathematician whose translation and commentary for Descartes’ landmark treatise, La Géométrie, led to the popularization of Cartesian geometry.
Descartes’ book was available in bookstores, but van Schooten’s work, Sive de Organica Conicarum Sectionum in Plano Descriptione, Tractatus (A Treatise on Devices for Drawing Conic Sections), remained tucked away in rare book collections. Luckily, Cornell’s Kroch Library contained a copy. David made the trip.
When he returned from the library, David could barely contain his enthusiasm. “Go and see it for yourself,” he said. “It’s really something.”
A visit to the library confirmed David’s findings. There in van Schooten’s book were drawing after drawing of devices that drew conics. The illustrations were exquisite, with artistic flourishes adorning many of them.
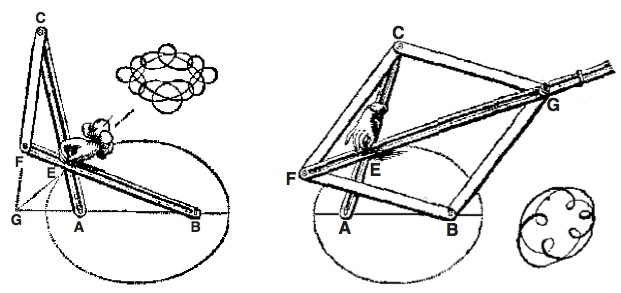
That was 1991. Today you can view van Schooten’s manuscript online.
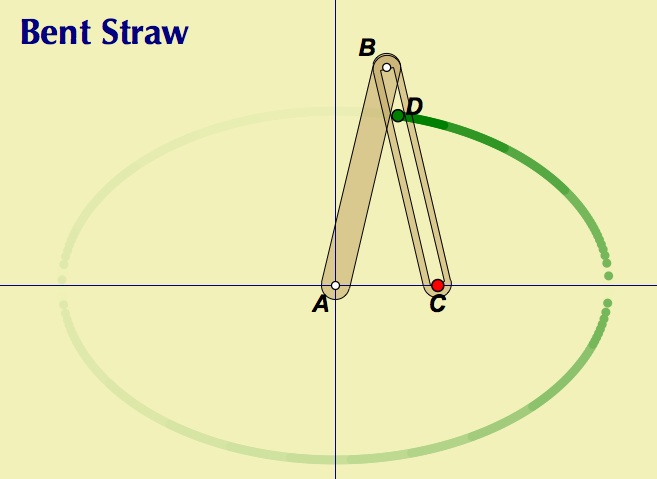
As I paged through van Schooten’s book, I wondered whether his ideas could find their way into mathematics classrooms. His models, consisting of hinges and slotted rulers, were not easy to build. How could students replicate them?
Sketchpad (and nowadays, Web Sketchpad) provided a large part of the answer. While nothing can substitute for the experience of operating a physical model, a Sketchpad simulation comes close. In fact, Sketchpad betters van Schooten in some ways, allowing students to manipulate the parameters of any model and view their effects on a curve immediately.
It’s been 20 years since I first developed van Schooten’s ideas into a Sketchpad module, Exploring Conic Sections with The Geometer’s Sketchpad, for Key Curriculum Press. I’ve just updated the book for its third edition with all-new sketches and revised activities. You can also interact with the models online using Web Sketchpad—just follow this link for other Sine of the Times posts featuring the conics.