This week, I’m going to describe one of my favorite activities for introducing young learners to multiplication and factors. It comes from  Nathalie Sinclair, a professor of mathematics education at Simon Fraser University.

In the interactive Web Sketchpad model below (and here), press Jump Along to watch the bunny take 2 jumps of 4 along the number line. The bunny leaves behind a trail of its path, providing a visual representation of 2 x 4 = 8.

With the bunny back at 0, it’s time to find other ways to reach 8. Enter new values for “Number of Jumps” and “Jump By.” Before pressing Jump Along, however, drag the red point that sits on the multi-colored segment. The color of this point controls the color of the bunny’s jumps. By making each set of jumps a different color, it’s easier to distinguish one from another, and the resulting rainbow-like pattern is an attractive artifact of students’ work.

Below are all four ways to reach 8. While students often meet the equivalence of a x b and b x a with a shrug, here we have a nice visual representation that distinguishes 2 x 4 and 1 x 8 from 4 x 2 and 8 x 1. We can also see the factors of 8 by noting where each of the four paths first lands on the number line (The red path, for example, lands first at 4, indicating that 4 is a factor of 8.)

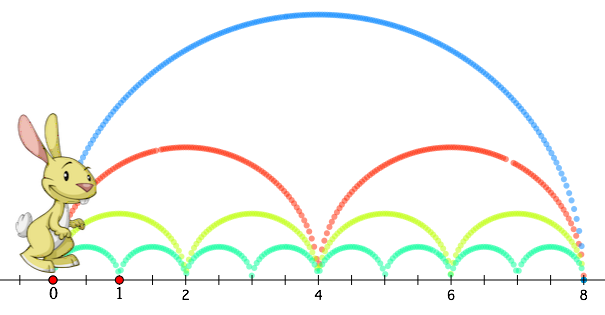Students can now explore other destinations on the number line. To  jump to numbers larger than 12, just drag the point at 1 closer to 0 to rescale the number line.

As students explore factor rainbows, they can explore questions like: Do certain numbers create prettier factor rainbows than others? For larger target destinations, are there more ways to reach the target? Which factor rainbows have only 2 paths? Do all factor rainbows contain an even number of paths?

An annotated list of all our elementary-themed blog posts is here.