Michael de Villiers teaches courses in mathematics and mathematics education at University of KwaZulu-Natal in South Africa. His website features a wealth of Dynamic Geometry-related books, articles, and sketches. He is the author of the Sketchpad activity module Rethinking Proof with The Geometer’s Sketchpad. This blog post is a condensed version of a longer article, “Conjecturing, Refuting and Proving Within the Context of Dynamic Geometry,” that will appear in the journal Learning and Teaching Mathematics (no. 17, December 2014).
–Guest post by Michael de Villiers
“Mathematics is about problems, and problems must be made the focus of a student’s mathematical life. Painful and creatively frustrating as it may be, students and their teachers should at all times be engaged in the process — having ideas, not having ideas, discovering patterns, making conjectures, constructing examples and counterexamples, devising arguments, and critiquing each other’s work.“ – Lockhart (2002)
Encouraging creative problem posing and problem solving in a mathematics classroom means that students will inevitably propose false conjectures that need to be refuted by counter-examples. The ability to refute or disprove false mathematical statements is in many ways as important as proving true ones, but is often neglected in teaching and learning.
This blog post describes a mathematical exploration that I recently undertook with a mathematical colleague, Nic Heideman. It highlights the dilation facility of Dynamic Geometry software and its role in refuting two very plausible conjectures. It follows on two iterative construction procedures described in De Villiers (2014) where iterated triangles converge towards an equilateral triangle.
Investigation 1: Tangent Points of Incircles
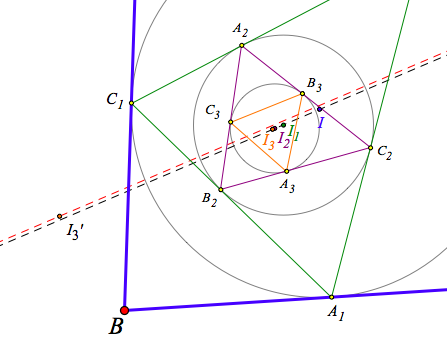
Start with any ΔABC and its incircle and incentre I. Label the points where the circle touches the sides BC, CA, and AB and respectively as A1, B1, and C1. Repeat the process with the new ΔA1B1C1 constructing the next incircle, I1.
Then repeat the process twice more. When you’re done, connect incentre I to I3 with a straight line. What do you visually notice about the four incentres? Check by dragging vertices A, B, and C in the interactive Web Sketchpad model below. Can you make a conjecture? Can you prove or disprove it?
Investigation 2: Excentres
Start with any ΔABC and construct its incentre I and excentres (The three excentres of a triangle are located at the intersection of the angle bisectors of the two exterior angles formed on each side of the triangle.) You can view this construction in the Web Sketchpad construction above by pressing the arrow in the lower-right corner of the screen.
Label the excentres formed on the sides of the sides BC, CA, and AB respectively as A1, B1, and C1, and construct incentre I1 of the new ΔA1B1C1. Repeat the process with ΔA1B1C1. Then repeat the process twice more. When you’re done, connect incentre I to I3 with a straight line. What do you visually notice about the four incentres? Check by dragging vertices A, B, and C in the Web Sketchpad model. Can you make a conjecture? Can you prove or disprove your conjecture?
In our first investigation, it clearly seems that all four incentres are collinear (lie on the same straight line), with I2 and I3 almost coinciding. The same seems to be true in our second investigation: Although I1 does not lie on the constructed line from I to I3, the other three incentres appear to be collinear. Using Dynamic Geometry software to drag our constructions convinced us that the conjectures were valid.
Armed with compelling experimental evidence that our conjectures were true, we proceeded to attack the two conjectures trying both geometric as well as algebraic approaches. Neither approach was immediately successful, with the algebraic approach becoming especially cumbersome and messy. Scanning the literature for any mention of the results, as well as other related mathematical results we might be able to use, also proved fruitless. While we did find that Denison (2001) describes the second conjecture as unproven, he incorrectly claims that all four incentres are collinear (Our Dynamic Geometry model illustrates that I1 is not collinear with the other three incentres.)
Refutation of Conjectures 1 and 2
Our frustrating inability to prove Conjectures 1 and 2 gradually led us to suspect that perhaps they were false, despite the seemingly convincing experimental evidence. So we went back to the proverbial drawing board to more closely examine the conjectures, this time trying to produce counter-examples to disprove them.
Since the incentre points were grouped so closely together, we clearly needed to enlarge the figures by zooming in. This could be achieved by dragging the entire figure to make it bigger and bigger. Alternatively, and more efficiently, we could use the dilation tool of the Dynamic Geometry software to enlarge relevant portions or elements of the figure to examine them more closely.
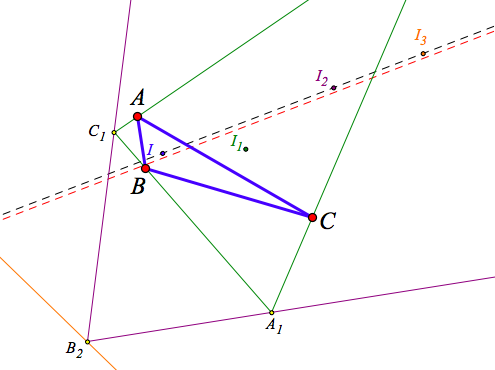
By marking I2 as the centre of dilation, and dilating the blue line through I and I3 as well as the incentres I, I1and I3, by a factor of 100 to 1, we noted that the line shifted to the dashed red line, as shown in the figure below (You can also press Show Dilated Objects in the Web Sketchpad model and then drag the dilation slider’s scale from 1 to 100. It might be necessary to drag the vertices of ΔABC to see the line clearly.)
Notice that the images of I and I3 still lie on the red line, whereas the image of I1 does not (Points I´ and I´1 are off screen, but in the software one can scroll up and to the right to check where they actually lie in relation to the enlarged, red line.) More over, despite I2 appearing to lie on the constructed blue line from I to I3, the line shift clearly shows that I2 is not on the line. Despite our strong, initial conviction, this showed conclusively that the incentres for Conjecture 1 were not collinear!
In the figure below showing Conjecture 2, we performed a similar dilation. Using I2 as our center of dilation, we dilated the dashed line through I and I3 as well as incentres I and I3 by a scale factor of 100. In doing so, the line shifted to the red dashed line and we can see that I2 does not lie along it (As before, you can also press Show Dilated Objects in the Web Sketchpad model and then drag the dilation slider’s scale from 1 to 100. You’ll need to drag the vertices of ΔABC to see the line clearly.) Note again that because of the large scale factor, images I´ and I´3 are completely off screen. Some scrolling, however, confirms that they are on the dilated red line.
Since the incentres lie so close to a straight line, it is important to emphasize that there is hardly any way we would have found these counter-examples by mere paper-and-pencil construction — unless, that is, we’d used a sheet of paper about 100 times the size of an A4 sheet, and were able to make accurate constructions using extremely large and unwieldy compasses and rulers! This episode therefore lucidly illustrates how useful computing software has become in modern day mathematical research, not only to find and formulate new conjectures, but also to enable one to disprove false statements with the production of counter-examples (compare De Villiers, 2010; Borwein, 2012).
References
Borwein, J.M. (2012). Exploratory Experimentation: Digitally-Assisted Discovery and Proof. In G. Hanna & M. de Villiers (Eds.), Proof and Proving in Mathematics Education, New ICMI Study Series 15, pp. 69-96.
Denison, B. (2001). Triangles & Quadrilaterals: A Response. Mathematics in School, Nov 2001, pp. 15-16.
De Villiers, M. (2014). Over and Over Again: Two Geometric Iterations with Triangles. Learning & Teaching Mathematics, No. 16, July 2014, pp. 40-45.
De Villiers, M. (2010). Experimentation and Proof in Mathematics. In G. Hanna, H.N. Jahnke & H. Pulte (eds.), Explanation and Proof in Mathematics: Philosophical and Educational Perspectives (pp. 205-221). New York: Springer.
Lockhart, P. (2002). A Mathematician’s Lament. In Devlin’s Angle (March 2008).