As readers of this blog can probably tell, I like puzzles. I especially enjoy taking ordinary mathematical topics that might not seem puzzle worthy and finding ways to inject some challenge, excitement, and mystery into them.

This week, I set my sights on isosceles triangles. It’s common to encounter isosceles triangles as supporting players in geometric proofs, but how can isosceles triangles be made the stars of their own mathematical puzzles?

Above is a collection of interactive Web Sketchpad puzzles. Each puzzle begins with an isosceles triangle ABC and a point R on the coordinate grid. Your goal is to drag a vertex of the triangle to point R so that the new triangle is also isosceles. In the first puzzle, this is easy: Dragging either vertex A, B, or C to point R results in an isosceles triangle.

Press the right arrow at the top of the sketch page to move on to the second puzzle. Point R now sits at (3, 2). This challenge is straightforward, too: Dragging point B to point R yields an isosceles triangle.

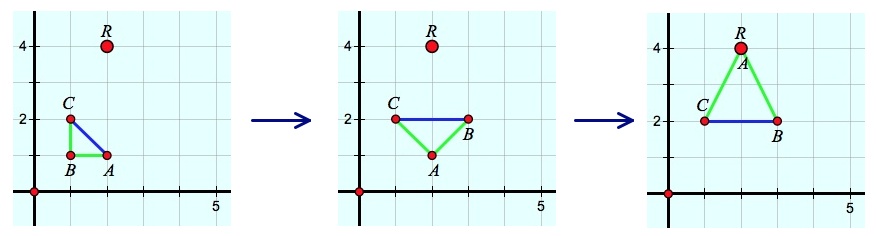
Pressing the right arrow again reveals the third puzzle, and this one is a little different. It’s no longer possible to drag vertex A, B, or C directly to point R while keeping ΔABC isosceles. We need to add a new rule to our puzzle: You can drag more than one vertex of ΔABC to reach point R, but each intermediate resting position of the triangle must be isosceles.

We can solve this particular puzzle in two steps: First,  drag point B to (3, 2). The resulting triangle is isosceles. Now drag point A to point R to solve the puzzle. Again, the triangle is isosceles.

 Most of the remaining Web Sketchpad puzzles above require multiple steps to position a vertex of isosceles triangle ABC at point R. As your students solve the challenges, here are some questions and tasks to present to them:

• Name all the locations for point R that allow you to solve the puzzle in just one move. Do these points, or a subset of them, share anything in common?
• Can you find the fewest number of moves needed to solve each puzzle?
• What general strategies did you discover for solving the isosceles triangle puzzles? Can you describe or illustrate these strategies so that a friend could follow them?
• Can you find a way to predict how many moves it will take to solve a puzzle without carrying out each step?
• On the second-to-last page of the Web Sketchpad model, pick your own location for point R and challenge a friend to solve your puzzle.
• On the last page of the Web Sketchpad model, find a sequence of moves for ΔABC so that one vertex of the triangle rests on point R and another vertex on point P.