According to Wikipedia, the Brouwer Fixed Point Theorem, named after mathematician and philosopher Luitzen Brouwer, states that “for any continuous function f mapping a compact convex set into itself, there is a point x₀ such that f(x₀) = x₀.

This is a deep theorem,  but one aspect of it is lovely, surprising, and entirely approachable by high-school geometry students.

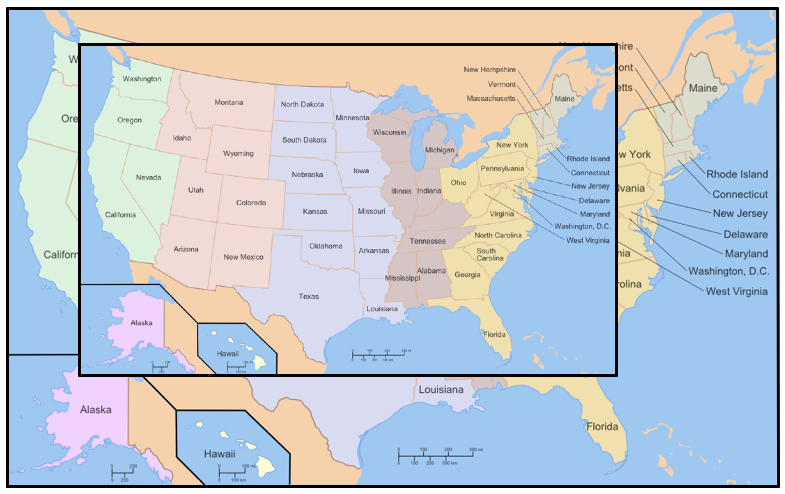
Below are two maps of the United States, one a scaled copy of the other. The smaller map sits atop the larger one, with the edges of both maps parallel (The scale factor and the particular location of the smaller map arbitrary.)

Believe it or not, you can stick a pin straight through both maps so that the pin simultaneously pierces the identical geographical location on each one!

Finding this special location (the “fixed point”) and proving that it satisfies this condition is possible with nothing more than a basic knowledge of geometry. Indeed, when I posed this challenge to teachers in my NYU geometry course, they devised a variety of clever proofs. In an upcoming post I’ll share their ideas, but for now, see what you and your students can discover.

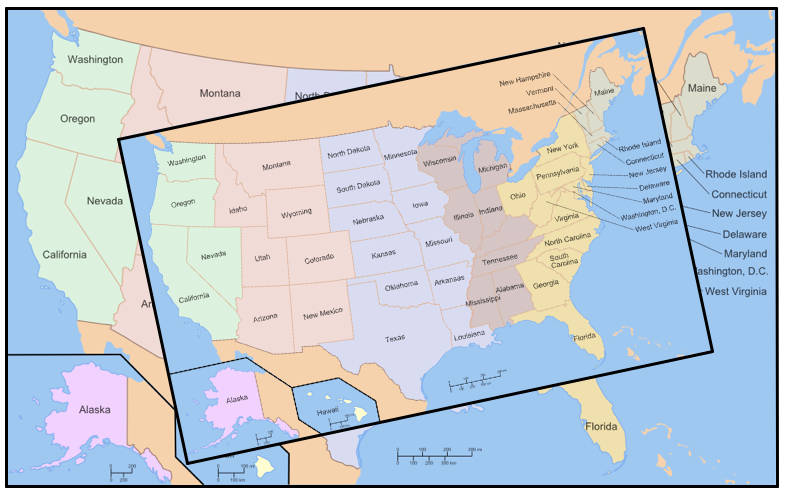
Meanwhile, let’s explore a variation of the map problem. Suppose that again we have two maps that are scaled copies, but rather than aligning their edges to be parallel, we simply place the smaller map randomly onto the other as shown below. It turns out that it is still possible to find a location for the pin that pierces the same spot on both maps simultaneously. Wow!

To aid us in finding this spot, let’s use Web Sketchpad. The interactive model below shows a digital artwork created by my mother, Joan Scher (If you’d prefer to work with the map, press the arrow in the lower-right corner of the sketch.) Change the value of n from 0 to 1. By doing so, you’ll create a rotated scaled copy of the painting placed on top of the original.

Now bump n from 1 to 2 and notice what happens. You’ll obtain yet another copy of the painting, created using the same shrink-and-rotate parameters, but this time applied to the scaled copy. Keep increasing the value of n. As you do, you’ll see a spiraling collection of scaled copies, built with the same shrink-and-rotate recipe. Try as well pressing “Repeated Copies” to watch n cycle from 0 to 30.

Can you convince yourself intuitively that this sequence of steadily shrinking pictures will converge to the “fixed point”  shared by the original two paintings?

To experiment more, you can adjust the scale factor (the “scale by” parameter in the sketch) and the amount of rotation (the “rotate by” parameter). You can also adjust the placement of the scaled copies by dragging the two small blue points that sit near the lower-left corner of the original picture.