I was happy to collaborate on this blog post with Dr. Stavroula Patsiomitou, a researcher at the Ministry of Education and Religious Affairs in Greece. Dr. Patsiomitou received her PhD from the University of Ioannina and has written extensively about the field of dynamic geometry environments, including Sketchpad and Web Sketchpad. Her textbook, Conceptual and Instrumental Trajectories Using Linking Visual Active Representations Created with The Geometer’s Sketchpad, was just published this year (in Greek). I was honored to write its preface.

Manipulatives are designed to mediate between a particular mathematical concept and the way pupils learn that concept. While historically the term “manipulative” has signified hands-on, “concrete” materials, numerous researchers have extended that definition to encompass computer manipulatives.

Cuisenaire rods are mathematical learning aids that were invented in 1945 by a Belgian primary school teacher, Georges Cuisenaire and popularized by Caleb Gattegno. They provide a hands-on way to explore mathematics and to learn such mathematical concepts as counting, the four basic arithmetical operations, working with fractions, and finding divisors. Here, we present several Web Sketchpad models of Cuisenaire rods.

The websketch below (and here), includes tools for building Cuisenaire rods of length 1 cm through 10 cm. Using the ONE tool, for example, creates a 1-cm rod. You can move the rod anywhere in the sketch and rotate it by dragging the point in its top-left corner. The tools allow you to make multiple copies of the same rod or build all 10 rods. And unlike the traditional Cuisenaire set, these rods are each divided to show the 1-cm unit rods that compose them.

Young learners deepen their understanding of numbers when they recognize that a quantity and its numerical representation form a one-to-one correspondence. In the websketch below (and here), the rods appear with numbers. The ONE tool, for example, creates a 1-cm rod with a “1” centered on it. The even numbers appear in yellow while the odd numbers are red, allowing students to visualize and categorize the numbers into two discrete sequences. 

Young learners can use the rods to model addition and build the same number in multiple ways, creating, for example, 9 = 7 + 2 = 6 + 3. They can also order the numbers with the rods to model inequalities like 1 < 2 < 3.

On page 2 of the websketch, the words ONE through TEN are included. Young learners can build the ten rods and then match them to their equivalent word. This task allows the children to connect the symbolic form of the number with its schematic and spoken expression.

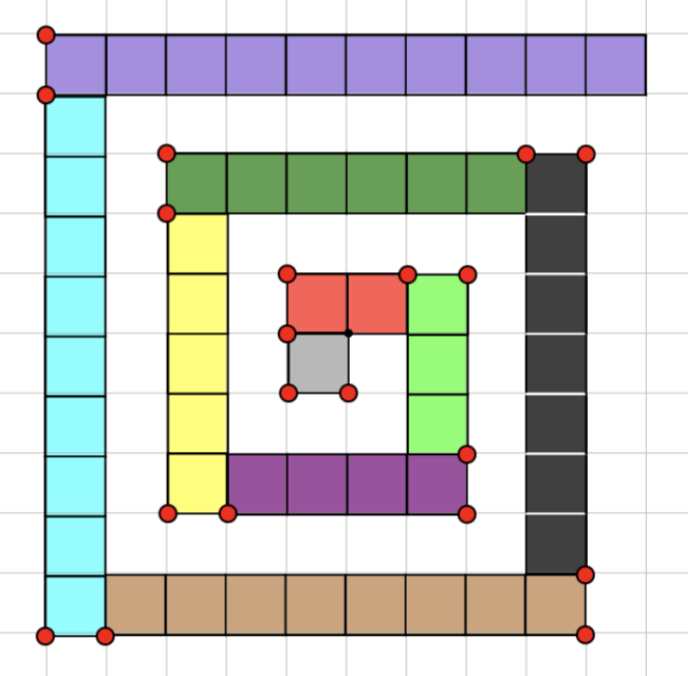
In the websketch below (and here) the inclusion of a rectangular grid opens more possibilities. Young learners might use the grid and the tools to create a spiral like the one below. They might also be given a square and be asked to use the rods to determine its area. Given the effort of filling the square with rods, children might then be motivated to reinvent multiplication as a simpler way to find its area.

These examples, as well as a multitude of other uses for the virtual Cuisenaire rods, demonstrate that the mindful use of technology by primary-school teachers can attract and engage children in such key areas as mathematical play, self-expression, and computational thinking. 

For more information about Cuisenaire rod models, be sure to check out this article by Stavroula Patsiomitou.