In the February 1954 issue of Mathematics Teacher, Paul C. Clifford describes an optimization problem from his trigonometry class. Of all isosceles triangles ABC with sides AB and BC of length 12, which one has the maximal area? Clifford told his class that an exact solution to the question required calculus. One student, … Continue Reading ››
Tag Archives: Web Sketchpad
Constructing Daisy Designs
With nothing but a compass, students can construct a lovely daisy design consisting of seven interlocking circles, all of the same size.
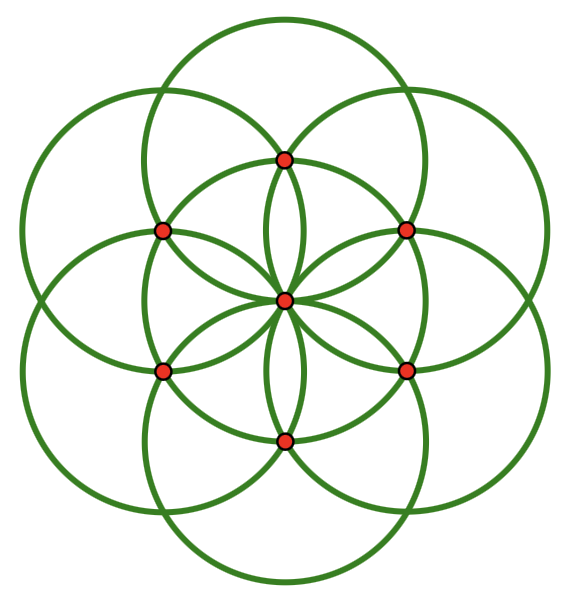
I was delighted to see that the U.S. postal service chose to feature … Continue Reading ››
A Geometric Interpretation of Euler’s Identity
While most numbers lead anonymous lives away from the mathematical spotlight, eiπ occupies hallowed ground. Douglas Hofstadter writes that when he first saw the statement eiπ = −1, “. . . perhaps at age 12 or so, it seemed truly magical, almost other-worldly.”
At the risk of deflating the celebrity status of … Continue Reading ››
Teaching with Web Sketchpad
This past semester, I taught a geometry course for teachers at City College here in New York. As you might expect, Sketchpad figured heavily in the course contents. But unlike other semesters when desktop Sketchpad was my tool of choice, this time, I took the plunge and limited myself to Web Sketchpad.
A Transformations Approach to Complex Numbers
This post, inspired by the work of Al Cuoco, uses Web Sketchpad to explore a transformations approach to complex numbers.
Slope of the Sine Function, Part 1
When I reached calculus in my senior year of high school, it was clear that it sat atop a mountain that I had been ascending ever since my Algebra 1 class. Without the tools and procedures I had amassed from algebra and precalculus, I could never have performed the symbolic manipulations necessary to … Continue Reading ››
Special Quadrilaterals and Their Diagonals
Given two segments and their midpoints, what quadrilaterals can you build using the segments as the diagonals of the quadrilateral?
The Origami-Math Connection
This post examines the connections between origami and geometry in the context of a new book written by Daniel Scher and Marc Kirschenbaum.
Virtual Cuisenaire Rods
I was happy to collaborate on this blog post with Dr. Stavroula Patsiomitou, a researcher at the Ministry of Education and Religious Affairs in Greece. Dr. Patsiomitou received her PhD from the University of Ioannina and has written extensively about the field of dynamic geometry environments, including Sketchpad and Web Sketchpad. … Continue Reading ››
A Bevy of Rhombus Constructions
In how many ways can you use dynamic geometry software to build a rhombus that stays a rhombus when its vertices are dragged? This challenge, a mainstay of Sketchpad workshops, invariably leads to great discussions because there are a multitude of ways to construct a rhombus, with each method highlighting different mathematical properties … Continue Reading ››