In the work that Scott and I have done with geometric functions, we’ve explored how geometric transformations can give students a window of understanding into functions that algebra alone may not provide. In this post, we turn to the role that transformations can play in making sense of complex number arithmetic. And as a bonus, by exploring the topic via transformations, we can make a lovely connection between complex number multiplication and two trig identities.
The sequence of activities that follows was inspired by the book Mathematical Connections by Al Cuoco and this handout from Avery Solomon, an instructor of mine at Cornell.
As you read the descriptions below, you may find it helpful to pause along the way and watch the YouTube video that I recorded to accompany the Web Sketchpad models..
Complex Addition
Our investigation begins by introducing two ways to identify the location of a complex number: through its rectangular form (x+ yi) and its polar form (r, θ). On page 1 of the Web Sketchpad model below (and here), students construct a complex number z with the Vector tool and measure its real and imaginary parts with the mRect tool. They drag the head of the vector and record what they notice and wonder when the head sits on the real axis, the imaginary axis, and in random locations on the complex plane. Students perform a similar investigation on page 2 by constructing complex number z, measuring its magnitude/length (r) and argument (θ) with the mPolar tool, and observing the effects of varying z.
On pages 3-6, students explore different ways to add two complex numbers, z and w. The tools on page 3 lead students to adopt a numerical approach to addition: They measure the real and imaginary parts of z and w, add the corresponding parts with the Calculate tool, and then plot the sum. On page 4, students explore a geometric approach, connecting complex addition to the process of adding two vectors. On page 5, students construct a parallelogram with z and w as adjacent sides to find the sum. And finally on page 6, students are given a streamlined Translate tool that they’ll use moving forward.
As students test their various addition constructions, they examine some special cases: adding two real numbers, adding two complex numbers, and adding a complex number to a real number.
Effects of Dilation
On pages 1 and 2 of the websketch below (and here), students explore the effects of dilating real numbers and pure imaginary numbers by a scale factor s. Having examined the special cases, they turn to an arbitrary complex number z. Viewing the rectangular form of z (page 3) highlights that dilating z by a scale factor of s multiplies the real and imaginary parts of z by s. And viewing the polar form of z (page 4) reveals that dilating z by s stretches z by a factor of ❘s❘. If s < 0, then there is both a stretch by ❘s❘ and a rotation by 180.°
On pages 5-7 of the websketch, students take two complex numbers, z and w, and use both the Translate and Dilate tools to construct –z, z – w, and 3z – 2w. To build 3z – 2w, for example, students use the Dilate tool to dilate z by 3 and w by -2. They then use the Translate tool to add 3z and -2w together.
Effects of Rotation
In the websketch below (and here) students explore the effects of rotating a complex number z by π/2, π, and 3π/2. Through some experimentation, students discover that rotating an arbitrary complex number z = a + bi by 90° about the origin yields –b + ai. Algebraically, this is equivalent to multiplying z by i. Students prove that multiplication by i is equivalent to rotation by 90° by using this illustration.
Complex Multiplication
The complex multiplication websketch (below and here) brings together all that students have learned about adding complex numbers, dilating them, and multiplying them by i.
On page 1, students construct 2zi by dilating z by 2 and then rotating 2z by 90°. On page 2, they construct z(1 + i) by first rewriting the expression as z + zi. They then rotate z by 90° to obtain zi and add it to z using the Translate tool.
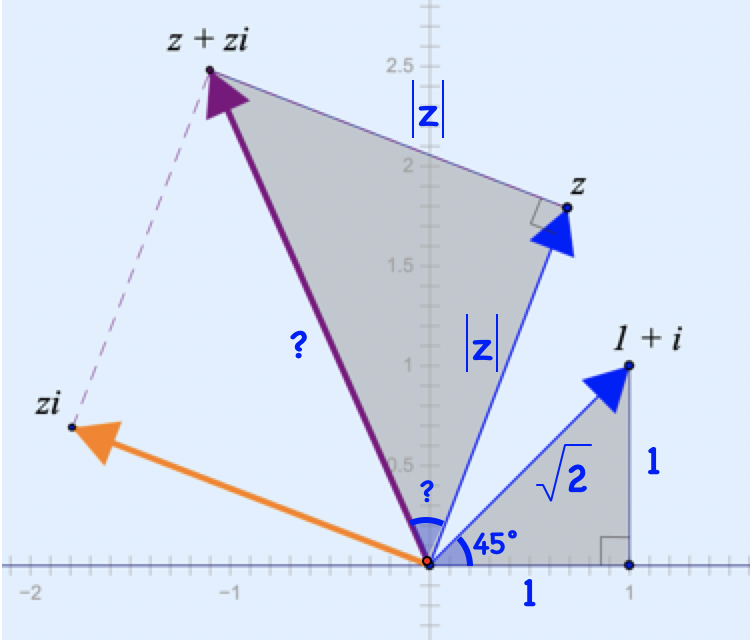
The picture below shows the product, z + zi, as well as two right triangles that have been added to the construction using the Right Triangle tool. The triangle whose hypotenuse is the vector 1 + i has lengths 1, 1, √2 and is an isosceles right triangle. By reviewing the construction steps they took, students can explain why the other triangle is also an isosceles right triangle. As such, the angle marked by a “?” is 45° and the length of z + zi is √2❘z❘. Thus the argument of z(1 + i) is the sum of the arguments of z and 1 + i and the length of z(1 + i) is the product of the lengths of z and 1 + i. Is this observation true in general when multiplying complex numbers?
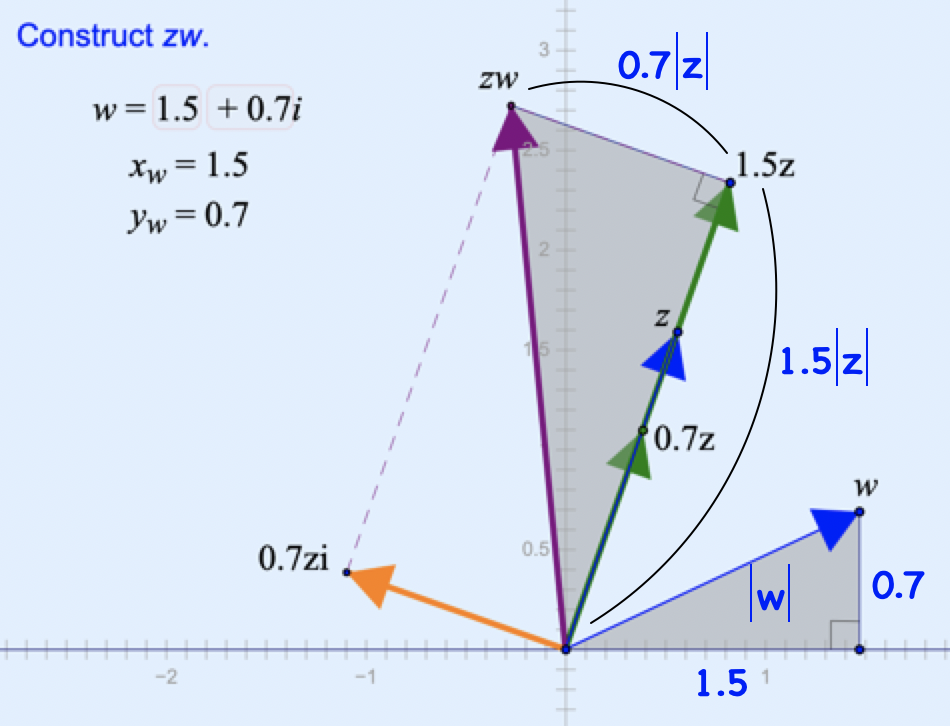
To investigate, students multiply two arbitrary complex numbers, z and w, on page 3. As before, they use the distributive property to rewrite the product. Specifically, zw = z(1.5 + 0.7i) = 1.5z + 0.7zi. The picture below shows the result of forming the product using the Dilate, Rotate, and Translate tools and then adding right triangles to the construction.
Students label the lengths of the two triangles that they know and prove that the triangles are similar. Can you see how this information allows them to geometrically prove the rule for multiplying two complex numbers—add the arguments and multiply the lengths? (The sketch also allows students to measure the arguments and lengths of z, w, and zw to provide informal numerical support for their proof. )
Complex Powers
In the sketch below (and here), students apply what they’ve learned about multiplying complex numbers to construct z2 and z3 from z. On page 1, to construct z2, they measure the length (r) and argument (θ) of z with the mPolar tool, compute r2 and 2θ, and plot (r2, 2θ) with the Plot(r, θ) tool. On page 2, given different tools, students construct z2 using transformations: They dilate z by r and then rotate rz by θ.
After constructing z3, students drag z to find locations for which z3 = 1. They use the mRect tool to express z as x + yi and then check that for each of the three locations for which z3 = 1, the algebra of cubing x + yi confirms the result (This is made simple by entering the expression into Google and letting it do the work).
Students can also explore the geometry behind solving z5 = 1, z6 = 1, z10 = 1, and z15 = 1 in this prior Sine of the Times post.
A Trigonometric Connection
A delightful outcome of proving the complex multiplication rule geometrically is that it allows us to derive trigonometric identities. Suppose z and w are two complex numbers on the unit circle. Let z = cos(θ)) + isin(θ) and w = cos(β) + isin(β). To find zw, rotate z by an angle of β (There is no dilation because ❘w❘ =1.) Thus, zw= cos(θ + β) + isin(θ + β). But we can also find zw by performing the multiplication with algebra:
zw= (cos(θ)) + isin(θ))·(cos(β) + isin(β))
= (cos(θ)cos(β) – sin(θ)isin(β)) + i(sin(θ)cos(β) + cos(θ)sin(β))
If both expressions are equal to zw, then the real parts must be equal as well as the imaginary parts. This means that:
cos(θ + β) = cos(θ)cos(β) – sin(θ)isin(β)
sin(θ + β) = sin(θ)cos(β) + cos(θ)sin(β)
How nifty—two trigonometric identities for the price of one! As the author Tristan Needham has written, “Every complex equation says two things at once.”