For the past year, I’ve collaborated with my longtime friend and leading origami artist Marc Kirschenbaum to author an origami book focused on topics from high-school geometry. Good news: our book is now available! You can read a review here.
We picked familiar topics from geometry such as angle measure, area, special triangles and quadrilaterals, tessellations, similarity, and the Pythagorean Theorem. We also wandered afield, offering an origami-inspired take on the Monty Hall problem and a whimsical approach to an infinite geometric series. Throughout, we aimed for an informal tone with an abundance of colorful images that would convey the artistic side of mathematics.
Below is a geometric representation of an infinite geometric series folded from a single square piece of paper that is orange on one side and yellow on the other. If the area of the overall square is 1, then the area of the theoretically infinite pattern of yellow squares is (1/4) + (1/4)2 + (1/4)3 + …
Notice that several origami bugs have gathered around the model and are pondering how it visually demonstrates that the sum of the series is 1/3. These bugs share the DNA of the folded geometric series: Inspired by the pattern of yellow squares, Marc took the geometric series model, added several extra folds to it, and, voilà! — a geometric series bug was born.
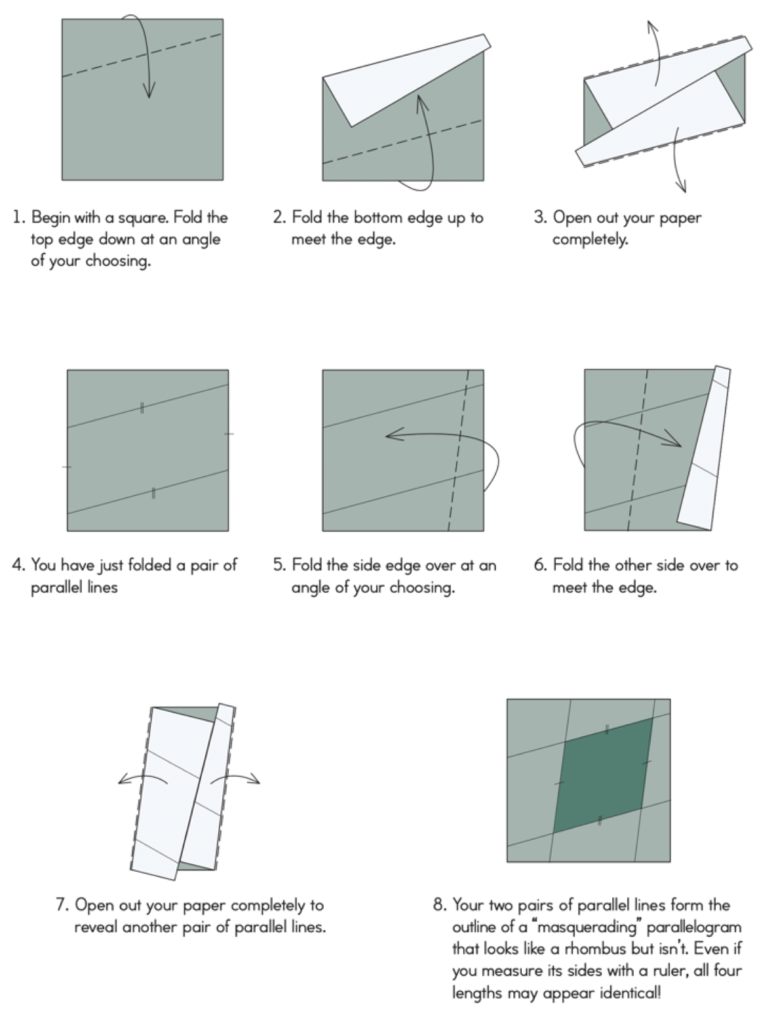
As we designed the origami models, we made unexpected mathematical discoveries. Consider the origami model diagrammed below. In steps 1-3, you fold the top and bottom edges of a square to meet. The two creases lines formed by the folds are parallel (step 4). Now, repeat this folding sequence with the right and left edges of the paper to form another pair of parallel lines (steps 5-7). What quadrilateral is outlined by the four creases in step 8?
We folded this model multiple times, picking different random creases in steps 1 and 5. Each time, our completed quadrilateral looked very much like a rhombus. Measuring its sides with a ruler seemed to confirm our suspicion.
But I didn’t trust our imprecise observations, so I turned (naturally) to Web Sketchpad and constructed a virtual model to accompany the folded origami. As you can see from the measurements below, quadrilateral ABCD is nearly a rhombus, but not quite. We have a parallelogram that is “masquerading” as a rhombus (Drag the red points along the square’s sides to experiment with different creases.) Starting with a square in step 1 biases the adjacent sides of ABCD to be nearly the same length. If you begin instead with a rectangle and follow the same folding sequence, the final quadrilateral will look much more like a parallelogram.
This is just one of many examples where connecting origami to familiar high-school math topics led to exciting discoveries that were new to both Marc and me. If you get a chance to fold models from our book, let us know what you discover!