In this lesson, one of my favorites from Exploring Algebra 1 with The Geometer’s Sketchpad, students model expressions with dynamic algebra tiles, using the areas of the tiles to see the equivalence of expressions in factored and expanded form.
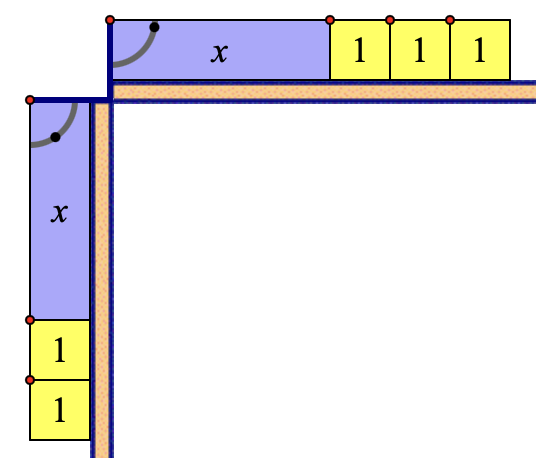
Down below (and here) is a Web Sketchpad model of algebra tiles. To model (x + 3)( x + 2), begin by using the 1 and x tools to create “trains” along the horizontal and vertical axes. Specifically, build an x + 1 + 1 + 1 train along the horizontal axis and an x + 1 + 1 train along the vertical axis (Drag the “flipper point” to change an x tile from horizontal to vertical.) These two trains define a rectangle with a length of x + 3 and a width of x + 2.
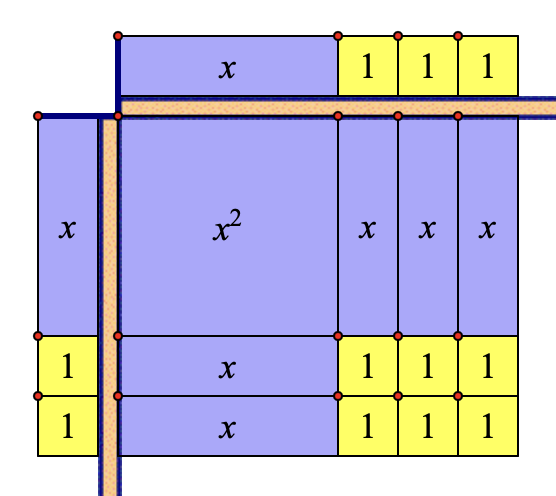
To construct the rectangle, use the 1, x, and x2 tools to fill the space. The algebra tiles below provide a visual representation of (x + 3)( x + 2) = x2 + 5x + 6. (A short video demonstrating the entire construction process is here.)
It’s important that students periodically drag the x and y sliders in the lower-right corner and show the numerical values of x and y. This is a big advantage of using Web Sketchpad algebra tiles since it reinforces the fact that x and y are variables, and that the relationships discovered work no matter what their values.
The page navigation controls in the lower-right corner of the sketch take you to additional blank templates that you can use to model other products like 3(3x), (x + y)2, and (2x + 3)(x + 3y + 1). You can also give challenges that work in reverse: For example, ask students to place one x2 tile, six x tiles, and eight 1s into the sketch. Now, challenge them to arrange the tiles into a rectangle and form the appropriate trains to display the length and width of the rectangle. By doing so, students will convert x2 + 6x + 8 into (x + 2)(x + 4).