Below are some common methods that geometry curricula offer for constructing scaled polygons:
- Place a polygon on the coordinate plane, pick the origin as the center of dilation, scale each vertex by some specified amount by using its coordinates, and then connect the scaled vertices.
- Draw rays from the center of dilation through the polygon’s vertices, put a point on one ray, and use this point as a vertex of the scaled polygon, constructing its sides parallel to the original polygon.
- Using dynamic geometry software, indicate the center of dilation, select the polygon, choose Dilate, and a scale factor. The scaled polygon appears instantly.
To complement these standard approaches, I’d like to present a fourth option, one that allows students to form the original polygon and its dilated image simultaneously rather than starting with the preimage.
In the Web Sketchpad model below (and here), begin by experimenting with the four directional arrows. By pressing them, you can move point A one unit to the left, right, up, or down. As point A travels, point B moves as well, mirroring the behavior of point A. Both points leave behind a trace of their paths.
To begin fresh, tap the Trace widget and then Erase Traces to clear the paths of the two points. Or, more simply, tap Reset in the lower-right corner.
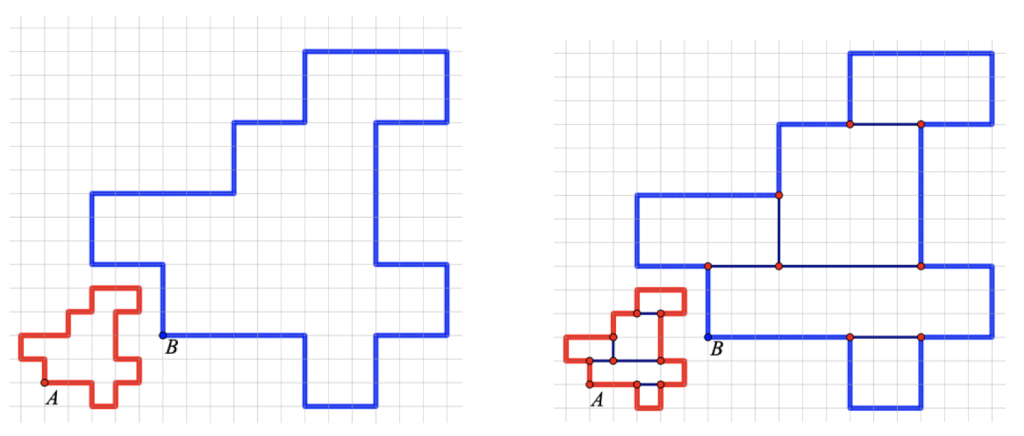
Now, enter a scale factor greater than 1. Once again, use the directional arrows to trace two polygons. The example below shows the result of choosing a scale factor of 3. The red and blue polygons are similar, with corresponding sides in the ratio of 3 to 1. Is the area of the blue polygon 3 times the area of the red polygon? Surprisingly no—the ratio of their areas is 9 to 1. One way to think about this is to use the Segment tool to deconstruct the blue and red polygons into rectangles and then consider the effect of scaling each rectangle’s sides by a factor of 3.
This activity gives students complete freedom in the polygons they draw, and there’s something undeniably fun (and, I hope, pedagogically beneficial) about watching the points move simultaneously at different speeds as they trace the polygons.