When students find the nth roots of a complex number, they use de Moivre’s Theorem and a fair bit of calculation and trigonometry. In this blog post, I’m going to approach the topic from a more visual perspective and make use of the following geometric way to think about complex number multiplication: To multiply two complex numbers, multiply their lengths and add their arguments (the angle they make with the positive real axis).
In the Web Sketchpad model below (and here), drag point z around the unit circle. As you do, notice that its location is given in both rectangular and polar form. Point z2 has the same length as z, but its argument is twice that of z. Thus when the argument of z is 45°, z2 is at i, making z = cos(45°) + i sin(45°) one solution to z2 = i. To leave a record of this solution, press Mark Location of z.
If you continue dragging point z counterclockwise around the unit circle, z2 moves twice as fast as z since its argument is twice as large. Thus when z travels 180° from 45° to 225°, z2 has moved 360°, back to its same location at i. This gives us the second solution to z2 = i. Press Mark Location of z again to leave a record of this additional solution.
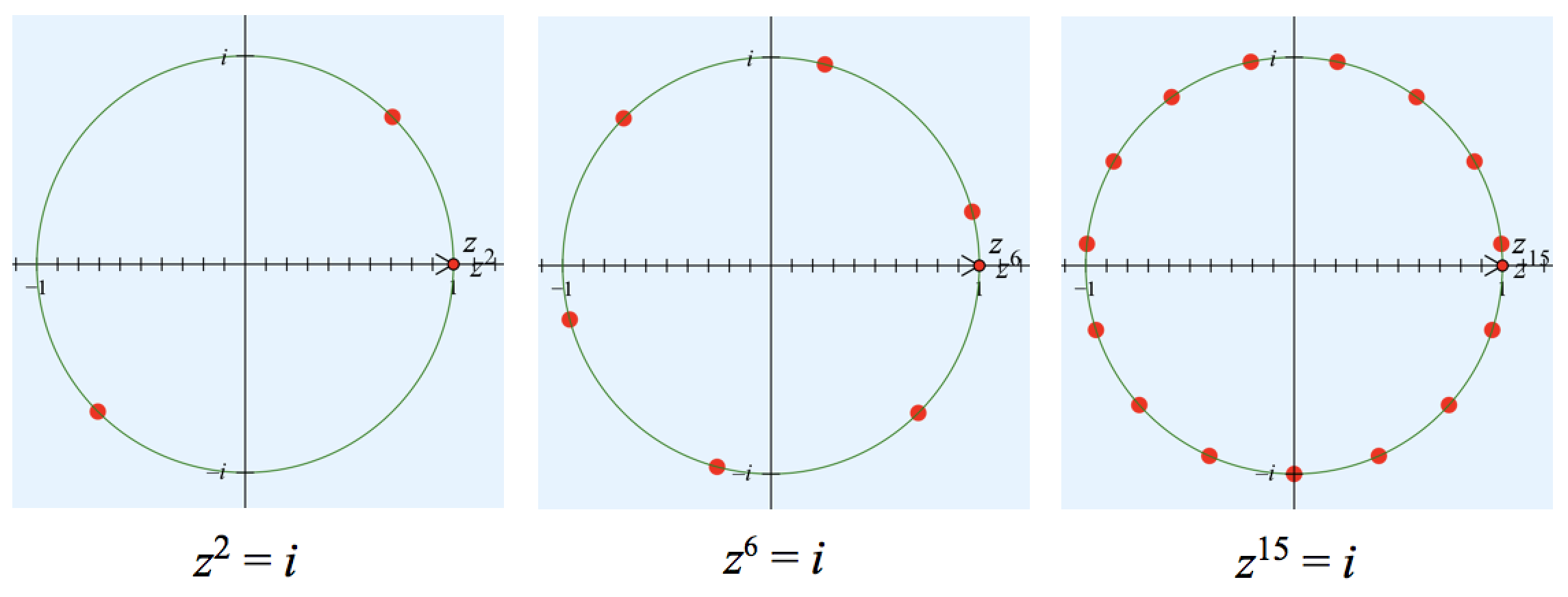
To solve z3= i, z5= i, z6= i, z10= i, and z15= i, use the page navigation arrows in the bottom-right corner of the websketch to move from problem to problem. For z6= i, notice that when z rotates 60°, z6 rotates 360°, explaining why the solutions to z6= i form the vertices of a regular hexagon. Below are the patterns formed for different powers of z, and for each, you can apply similar reasoning to make sense of the spacing of the points on the unit circle.