I was delighted that Daniel recently posted our Binomial Multiplication sketches in Web Sketchpad format. I thought about those sketches when I noticed a fairly new myNCTM thread on “When and How do we phase out the body in math education?”

This thread raises a very important question for us as teachers: How can we do a better job of relating math to students’ bodily experiences? The evidence supporting “embodied cognition” and/or “enactivism” is quite persuasive about how our abstract mathematical concepts arise from the interplay between our senses (vision, hearing, touch, etc.) and our actions. So the extent to which we “phase out the body” prematurely hinders our students’ efforts to learn the math we’re trying to teach them.

There’s a related issue: even if we provide students with concrete experiences related to the concepts we’re teaching, they may have trouble connecting those experiences with the concepts. In this paper the authors “argue for an approach that begins with concrete materials and gradually and explicitly fades toward more abstract ones.” To follow this approach (usually termed “concreteness fading” or “progressive abstraction”) we need to be thoughtful and gradual about when and how we “phase out the body.”

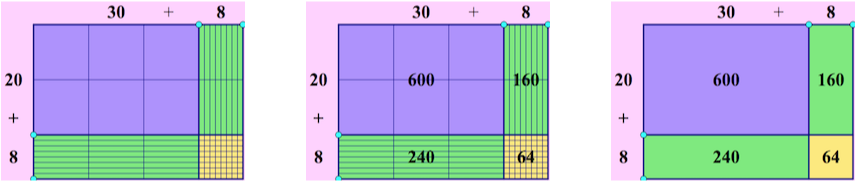
This is what we tried to do in our Binomial Multiplication activities. It’s not uncommon for algebra students to start with algebra tiles, end with FOIL, and never connect the two. We designed a sequence of sketches to try to bridge that gap, by beginning even earlier (and more concretely), using base ten blocks to show two-digit multiplication. The first step of concreteness fading occurs when students move from physical tens blocks to the virtual blocks on the computer screen. Instead of counting out individual units, rods, and flats, and lining them up, they drag sliders to make the blocks appear, already arranged, as in the image on the left. In the second image the partial product for each of the four regions appears, superimposed on the region. This adds a layer of abstraction, but it’s still easy to see that the top left region contains six hundreds flats. In the third image that concrete connection fades away, leaving more abstract connections, the first of which is that two tens multiplied by three tens produces six hundreds (Click any of the images to open a dynamic Web Sketchpad model.)

By now you’ve probably guessed the next fading step: we’ll fade the connection between the units and the rods so that a rod doesn’t have to be ten units. This won’t be the first time students have heard the term “variable,” but physically dragging a slider labeled x tends to make that variable a bit more concrete than just seeing the letter x on paper.

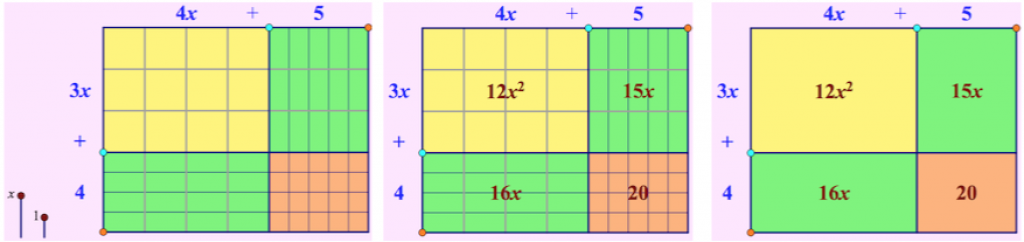
The fading steps are essentially the same for binomial multiplication as they were for two-digit multiplication, a remarkable opportunity for students to connect the structure of multiplication in arithmetic and algebra. A second binomial multiplication sketch allows the units sliders to move in negative as well as positive directions.

As a next step, where students turn the process around by expressing a trinomial as the product of two binomials, we begin with even more fading of the multiplication model to prepare them for a Factoring Game activity.

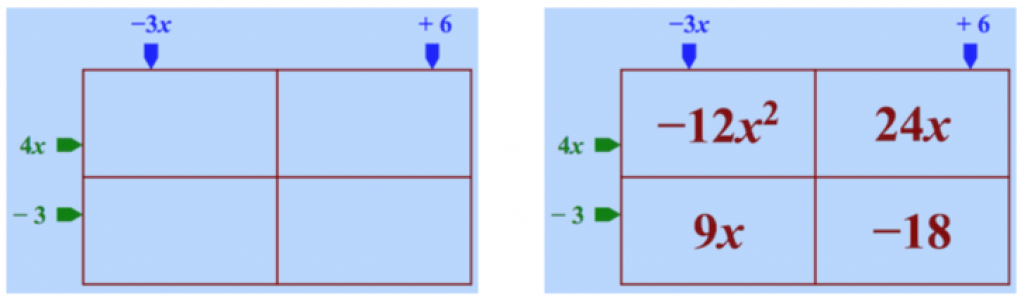
I mentioned FOIL earlier—but FOIL is a dead end: it makes no connection to two-digit multiplication or to multiplying a binomial by a trinomial. (See Nix the Tricks chapter 7.) The visual image makes FOIL obvious: you could just write the letters F, O, I, and L in the four boxes. (But if you actually do this, do it as part of your explanation of why FOIL is bad: it adds confusing clutter while making it harder to extend the method to higher-order polynomials.)

The websketches described in this blog post are freely available to use with your students and were originally created with The Geometer’s Sketchpad as part of our Dynamic Number NSF project. It’s a labor of love for us to convert them to Web Sketchpad and make more and more of them freely available on the web.