Metamorphosis is a New York-based company that offers professional content coaching to transform the mindset and practice of both teachers and administrators. I recently had the pleasure to collaborate with Metamorphosis staff members Toni Cameron and Kara Levin as well as mathematics coach Ariel Dlugasch from P.S. 276 in a coaching learning community that brought together mathematics coaches to explore tessellations.
We began the session by introducing the coaches to a Web Sketchpad model that allowed them to create regular polygon tessellations. You can try it yourself by clicking the image below to open the accompanying Web Sketchpad model. (A movie at the end of this post demonstrates how it works.)
As they explored the model, the coaches determined which regular polygons tessellated the plane and which ones did not. They posed questions to each other, made conjectures, tested theories, and thought about the big mathematical ideas of the investigation.
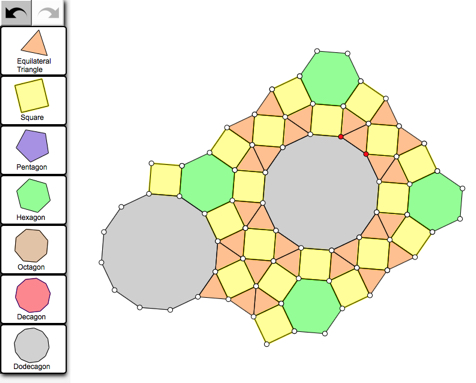
The coaches determined that the equilateral triangle, square, and hexagon could tile the plane. They noticed that because six equilateral triangles converged at a single vertex, they could determine the angle measure of each triangle by dividing 360° by 6. They made a similar observation about the angles of hexagons.
The coaches then returned to the Web Sketchpad model and investigated which combinations of regular polygons could tile the plane. Above is an example of a particularly attractive tessellation discovered by a coach.
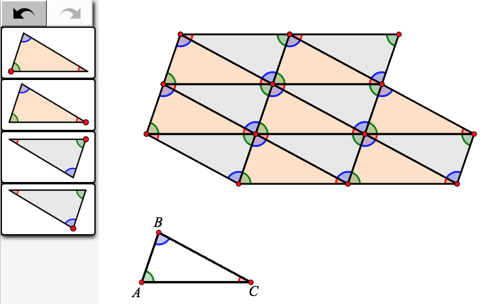
The coaches then turned their attention to arbitrary triangles. The Web Sketchpad model below (again, click the image to open it) starts with a triangle ABC and provides tools for snapping copies of ΔABC together in either its initial orientation or as a rotated copy (Again, the movie at the end of this post explains how the tools work.) What’s especially nice about this model is that after you’ve built a tessellation using a specific triangle, you can then drag any vertex of ΔABC and the entire tessellation will reshape itself to match the new triangle.
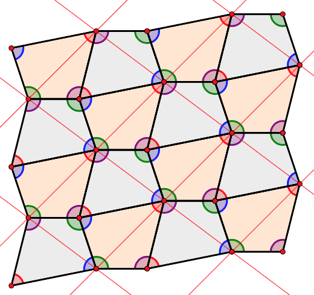
By experimenting with the tessellated triangles, the coaches noticed that the three angles of the triangle always came together at a vertex to form a straight line—a very elegant and memorable demonstration that the angles of an arbitrary triangle sum to 180º.
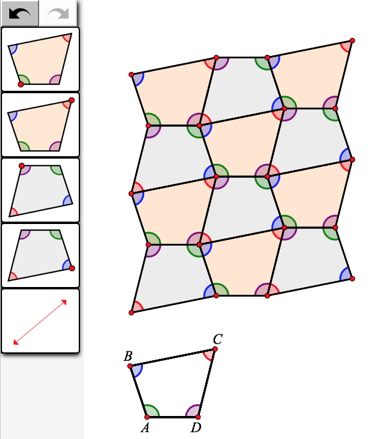
Finally, the coaches investigated whether arbitrary quadrilaterals could tessellate. As before, a Web Sketchpad model (click below to open it) made it easy to experiment with different quadrilaterals simply by dragging the four vertices of quadrilateral ABCD. Building on their observation about triangle angles, the coaches discussed how their quadrilateral tessellations demonstrated that the angles of a quadrilateral sum to 360º.
Time was running short since the coaches needed to plan the afternoon session in which fifth graders would try the regular polygon tessellation websketch. As such, the coaches did not have a chance to use the line tool that accompanied the four quadrilateral tools. But try it yourself, using it to connect vertices in your quadrilateral tessellation that lie on a line. In the illustration below, the lines form a tessellation of parallelograms. You can imagine these parallelograms, each with the identical pattern of four triangles, serving as another way to create the same pattern.