For the past year, my blogging partner Scott and I have worked with the team of Everyday Mathematics to build interactive Web Sketchpad models for their forthcoming new edition. It’s been fun for both of us to find ways to insert dynamic mathematics into their K–6 curriculum. Last year, I shared an Everyday Mathematics isosceles triangle investigation that featured a unique use of virtual protractors. Now I’d like to show you two Everyday Mathematics-inspired Web Sketchpad models that focus on triangle area.
Depending on how it is introduced, triangle area can be either dull and formulaic (“To calculate a triangle’s area, multiply its base by height and divide by 2”) or it can be an opportunity for discovery and critical thinking. As I would expect, Everyday Mathematics opts for the latter approach.
Below is a triangle. Put yourself in the shoes of an elementary-age student who doesn’t know the formula for triangle area but does know how to compute the area of rectangles. Can you use the draggable and resizable rectangles provided with the model to help compute the triangle’s area?
Below is an approach that a student might take, enclosing a triangle with the two rectangles. Notice that the rectangles divide the overall triangle into two right triangles. By visual inspection, it’s clear that the area of each right triangle is half the area of its associated rectangle. Thus the area of the entire triangle is 1⁄2 (4·2) + 1⁄2 (4·5), or 14 square units. By pressing New Problem and experimenting with other triangles (all of which have a base along the grid lines), students develop on their own the area formula for right triangles. Indeed, students may begin to suspect that this formula applies to all triangles, not just those with right angles
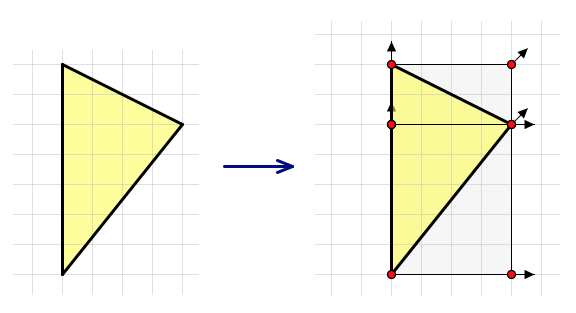To continue their investigation, students press the arrow button in the lower-right corner of the sketch to move on to a new page of problems. These problems are of the same type as those they just solved, but with one difference: the dimensions of the two rectangles are provided. Since students have already determined that the areas of the rectangles are essential for finding the triangle areas, pedagogically it seems reasonable to now save them the effort of counting squares.
The third page of the interactive model above switches to a different type of challenge. As before, the goal is to use one or more of the rectangles to help determine the area of the triangle, but now, the triangle only occasionally has a base that sits along the grid lines.
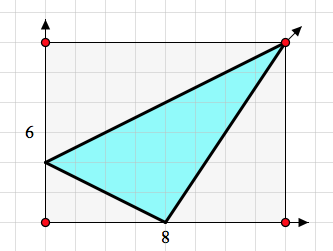
In the example below, a student has enclosed a triangle with a single rectangle whose area is 8·6, or 48 square units. To determine the area of the blue triangle, the student realizes that she can subtract the areas of the three right triangles from the area of the rectangle. Thus the area of the blue triangle is 48 – 1⁄2 (4·2) – 1⁄2 (8·4) – 1⁄2 (4·6), or 16 square units.
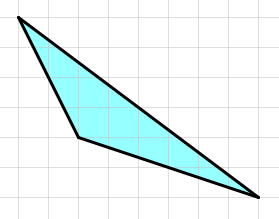
I’ll leave you with one last question: How might you adapt this method to find the area of the triangle below?
This is a new way of investigating the area of a triangle. I’ve not tried teaching it in this way before, but I think I will try it next time I have the opportunity. Thanks for sharing!