Algebra classes devote considerable time to equations in a single variable before solving multiple equations in two or more unknowns. But just because elementary-age students are not familiar with algebraic symbolism doesn’t mean they can’t solve simultaneous equations, too!

The mathematician and educator W. W. Sawyer makes a compelling argument for the early introduction of simultaneous equation in his 1964 book, Visions in Elementary Mathematics:

It is quite possible to use simultaneous equations as an introduction to algebra. Within a single lesson, pupils who previously did not know what x meant can come not merely to see what simultaneous equations are, but to have some competence in solving them. No rules need to be learnt; the work proceeds on a basis of common sense. The problems the pupils solve in such a first lesson will not be of any practical value. They will be in the nature of puzzles.

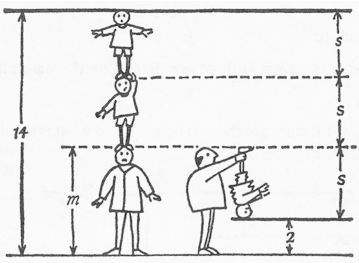
Sawyer gives an example of such a puzzle, stating that “a man has two sons. The sons are twins; they are the same height. If we add the man’s height to the height of one son, we get 10 feet. The total height of the man and the two sons is 14 feet. What are the heights of the man and his sons?”

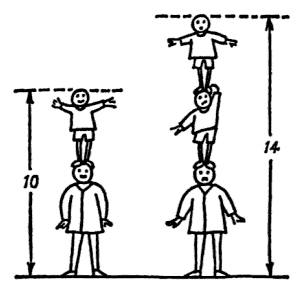
This puzzle amounts to a simultaneous equation, but by looking at the illustration at right, it’s clear—even to a young child—that the sons are 4 feet tall and the man is 6 feet. Another example from Sawyer is below.

Inspired by Sawyer’s work, I designed my own simultaneous equations puzzle for elementary school students as part of the Dynamic Number project. An interactive Web Sketchpad version of the puzzle appears below (and here).

Each square in the 4 x 4 grid is randomly populated with either a circle, triangle, square, or hexagon, or is left blank. Each of the four shapes is assigned a secret numerical value between 1 and 10. Students can view the sum of the shapes in any row or column of the grid simply by pressing the corresponding Show Sum button. The goal is to determine the numerical values of the shapes by reasoning about the sums and to do so in as few button presses as possible.

Each time students press New Problem, a new assortment of random shapes appears in the grid and the numerical values of the shapes change as well. Some challenges are harder than others depending on how many blank squares appear in the grid. Students might discover, for example, that a square and a circle sum to 13 while a square and two circles sum to 17. Reasoning that the two sets of shapes are the same except for the extra circle, students can deduce that the circle is equal to 4 (just as they might reason about the height of the son in Sawyer’s puzzle).

Because there are a total of eight rows and columns in the grid, students have lots of options for picking which sums will be most helpful. And if a particular grid proves too hard to solve, no big deal—students can simply press New Problem and try again.

On the second page of the websketch, students to set their own numerical values for the four shapes. Working in pairs, one student looks away while the other student enters values for the four shapes. When she’s done, she presses Hide Answers and then New Shapes, perhaps more than once, until she’s satisfied with the difficulty level of the puzzle. Her partner then gets cracking on the solution.

An annotated list of all our elementary-themed blog posts is here.