Simultaneous equations belong in elementary-school mathematics curricula. That’s been my mantra for many years, and I want to examine it now in the context of an interactive Web Sketchpad activity.

When I say that elementary-age students should encounter simultaneous equations, I don’t mean that they should be instructed in the standard algebraic procedure for solving pairs of equations like x + 2y = 9 and 3x – y = –1. Rather, my interest lies in presenting students with puzzle-like situations in which they solve for multiple  unknown values by using their common sense (You can see two interactive Web Sketchpad models of this approach here and here in my prior posts.)

Take a look at the interactive Web Sketchpad model below (and here). It displays eight rows of shapes, each containing a different combination of circles and squares. Pick a row and drag the shapes across the vertical divider line. When you do, the sum of those circles and squares will appear in the right-hand column. The goal is to determine the numerical values of the circle and square.

When I’ve observed this activity in classrooms with third, fourth, or fifth graders, students usually begin by taking a guess based on what they learn about a single row. For example, dragging the top row of shapes, the square and circle, across the vertical divider reveals that square + circle = 9. Might the square equal 8 and the circle equal 1? Students check by dragging another row of shapes across the divider. Two squares plus a circle equals 11, but 8 + 8 + 1 does not equal 11. Trying other values for the circle and square soon reveals that square = 2 and circle = 7. The puzzle is now solved, but students are not finished: They find it fun to predict the sums of the other rows before dragging each across the vertical divider. This helps to drive home the message that every circle in every row shares the same value, as does every square—something that’s not always clear to students.

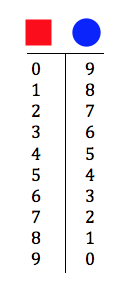
With a little guidance, students become more systematic in their approach to solving the puzzles. For example, knowing that circle + square = 9 means that there are 10 possible pairs of values for the two shapes. Students list these in a table like the one below and then check to see which pair of values satisfies the sums of the other combinations of shapes.

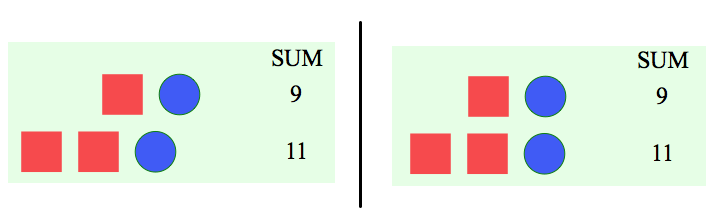
One aspect of this puzzle that I especially like is that students can choose how far across the vertical divider to drag each row of shapes. Below are two different placements for the first two rows of shapes.

The placement of the shapes on the right invariably encourages a student to make a key discovery: The shapes in both rows are nearly the same. Both contain a square and a circle, but the second row contains one extra square. That must mean that the square is equal to 11 – 9 = 2. Since the square equals 2, the circle must equal 7.

Using common sense, the student has just done—and explained—some important algebra! A problem like this can support a stimulating number talk (algebra talk?) that encourages many students to participate by describing their own numeric and proto-algebraic thinking.

Here are some of the interesting discussion questions that naturally arise when students work with this puzzle:

• Is it always possible to determine the values of the circle and square regardless of which two rows we pick?
• Which pairs of rows make it easy to solve for the circle and square? Which pairs of rows make it harder?
• Might there be more than one answer to a puzzle?
• Could a puzzle exist that has no answer?

Use the arrow buttons in the lower-right corner of the web sketch to navigate from page to page. The second page looks just like the first, but now, the possible values of the circle and square range from 0 to 20 rather than from 0 to 8. The third page of the sketch allows students to create problems for each other, deciding for themselves what values to assign to the circle and square (Should the circle equal 3,452? Should it equal –28? Students create far harder problems for each other than we might create for them!) The fourth page of the sketch adds a third symbol to the mix—a triangle—and now students must solve for three unknowns. The final page of the sketch allows student to create their own problems with three unknowns to share with each other.

If you have a chance to use this activity with your students, I’d love to hear what discoveries they make!

An annotated list of all our elementary-themed blog posts is here.