In a prior blog post, I presented an uncommon method for solving the well-known Burning Tent problem. My solution, modeled on the approach in the Connected Geometry curriculum, used a dynamic ellipse to pinpoint the optimal solution. Now, I’d like to offer a related problem from Connected Geometry where the pedagogical benefit of using an ellipse becomes even clearer. Here is the situation:

You (at point Y) and your friend (at point F) are floating on inflatable lounge chairs in a circular swimming pool. You want to paddle to the edge of the pool to leave your sunglasses there, and then swim to your friend. Where should you paddle to minimize the total distance?

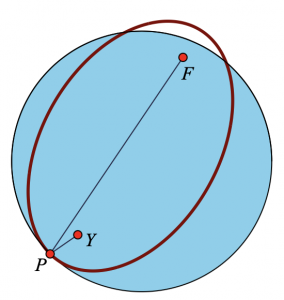
Page 1 of the Web Sketchpad model below (and here) shows the pool as well as points Y and F. Point P is a possible location where you might swim. You can drag point P around the circumference of the pool.

Notice that the model also includes an ellipse. The ellipse has foci at points Y and F and passes through point P. All the points on the ellipse are locations that are equally good (or bad) as swimming to point P.

Drag point P around the pool and watch as the ellipse grows and shrinks. Can you identify some interesting locations for P? In particular, notice when the ellipse is tangent to the circle. What do you think makes those locations noteworthy?

Now go to page 2 of the websketch, using the arrow in the lower-right corner). You’ll see the same swimming pool, but now there’s a graph showing the location of point P on the pool’s circumference plotted against the total distance to swim. As you drag point P, notice the locations where the ellipse is tangent to the circle and how those correspond to significant points on the graph. (When using this activity with students, I’d first ask them to sketch a graph themselves on a large sheet of paper before showing them the pre-made graph.)

This exploration introduces notions from calculus such as absolute minimum, absolute maximum, local minimum, and local maximum all without any algebra or reliance on derivatives. For example, when point P sits at the local minimum of the graph, the ellipse is tangent to the circle, with those points to the right or left of P on the pool’s circumference sitting outside the ellipse (see the picture below). Thus point P is a better place to swim than any of those nearby points. However, point P is not the absolute best place to swim because there are locations on the other side of the pool that are inside the ellipse. By examining the ellipse in relation to the pool’s circumference, students can explain why a location of point P is an absolute minimum, absolute maximum, local minimum, or local maximum without even seeing the graph.

You can change the graph by dragging points Y and F to new locations. Can points Y and F be positioned so that there are: (i) two locations of point P that produce the absolute minimum? (ii) no locations of point P that produce the absolute minimum? (iii) no locations of point P that produce a local minimum?

On page 3 of the websketch, the pool is now rectangular, leading to an even more interesting graph.

March 2025 Update

I’m preparing the syllabus for my geometry class at City College this fall, and as much as I love the Swimming Pool problem, I will confess that I have been hesitant to include it in my curriculum. That’s because many students don’t seem to understand the role that the ellipse plays in helping to identify the local and absolute min/maxes of the graph. In thinking about how I could adapt the lesson, it occurred to me that perhaps I needed to start with a simpler problem, one in which students use a circle rather than an ellipse to visualize the shape of the graph.

Here is my plan: I’ll begin by asking students to imagine that they’re standing in a triangular swimming pool at point Y (see page 1 of the websketch below (and here)). Using the Compass tool, can they find the shortest distance to swim from point Y to the edge of the pool? My hunch is that students will, without assistance, construct a circle centered at point Y and then drag the point on its circumference to form the smallest circle tangent to a side of the triangle.

I’ll continue by asking the class to drag point Y to a new location for which there are two equally good spots to swim. And as a way of introducing the incenter of a triangle, I’ll challenge them to place point Y so that three equally good spots exist. To conclude, I’ll ask them to find the spot that would require them to swim the farthest to reach the pool’s edge.

Page 2 of the websketch below shows a graph of the location of point P on the pool’s circumference plotted against the total distance to swim. As with the ellipse version above, this model introduces students not only to absolute minimum and maximum, but local minimum and maximum as well.

My hope is that by using a circle rather than an ellipse to judge distances, this will provide a gentler introduction to geometric optimization and pave the way for the ellipse version that will follow it. Am I too optimistic? I’ll let you know this fall!