A Double Spiral from David Henderson
David Henderson, the author of Experiencing Geometry, died this past December. I wrote about David in a prior post, and in particular, his approach of asking us to grapple with a small number of rich problems, allowing us to find our own, often non-traditional, ways of solving them over weeks at a time. In this post, I’d like to share one of David’s problems that he posed to us in Math 408 in 1991. It’s a lovely question, and one that I have not seen elsewhere.
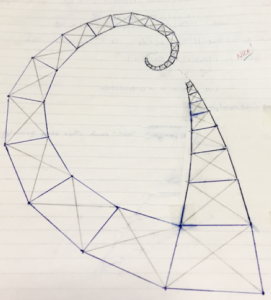
Start with a quadrilateral ABCD. Create a scaled copy A’B’C’D’ so that when A’B’ is placed onto side CD of the original quadrilateral, the two sides match up (see below). Repeat this process over and over again, scaling each new quadrilateral by the same amount and attaching it the growing spiral of similar quadrilaterals. Then start over, repeating the same process to build a spiral onto side AC of the original quadrilateral using a scale factor of AC/BD.
Assuming that DC < AB and AC < BD, the two spirals converge in a point. Can you prove it? I recommend placing the double spiral on the complex plane and representing the transformations of quadrilateral ABCD in terms of complex number arithmetic (If you need a hint or would like to see how others approached the problem, read the blog feedback below and James Tanton’s two proofs, one and two).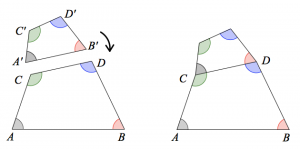
In 1991, we did not have dynamic geometry software that could easily build such a construction, so David asked us to cut out a quadrilateral and use it to draw as much of the two spirals as we could. Below is my illustration. Can you figure out how I might have used my paper quadrilateral to create the spirals?
Now, 27 years later, I’m able to not only construct the spirals easily and accurately with Sketchpad, but I can also drag the vertices of ABCD to watch the spirals react dynamically. Try it below (or here) with the Web Sketchpad model.
If you are interested in reading more about David, I recommend this Cornell Chronicle obituary. And this Flickr account shows pictures of David taken throughout his life.
I’ll close with a quote from David’s course syllabus:
JULY 2019 UPDATE: David’s double-spiral construction has been quite a hit! Suzanne von Oy extended the spiral pattern with Desmos, @jagarikin created two animations of the spirals (one and two), and this spiral from Vincent Pantaloni features Spiderman!
