[Today’s post is from Steven Fuchs, with whom I recently corresponded and whose enthusiasm was sufficiently infectious that I pressed him to share it here. –Scott]

One day late last spring, while teaching at St. Thomas High School in Houston, I noticed in a book a figure demonstrating Monge’s Theorem. (Don’t look this up yet; it’s much more fun to explore yourself than to read somebody else’s statement of it.) Monge’s theorem was unfamiliar to me but is easy to find on the web, and put me in mind of a saying of a professor of mine: “it is well known, to those who know it well.”

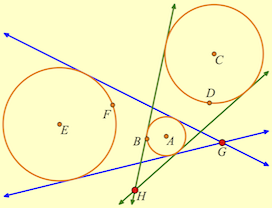
Given two circles of different radii where one doesn’t enclose the other, the two external tangents intersect in a point. If you have three such circles and consider them in pairs, there are three points of intersection. Monge’s theorem describes the relationship among these intersections. I encourage you to work on the construction and discover the relationship yourself. The figure on the right shows two of the three pairs of tangents; you will need all three for your investigation. [Figuring out how to construct the external tangents to two given circles is the challenging part for most people. This sketch provides hints, but don’t peek till you’ve worked on it for a while. Alternatively, take a look at the movie about this challenge from a post of mine last year. –Scott]

Thrilled by the surprising result, I built the sketch that night to show all my students the next day. Though it related to the subject of only one of the courses I was teaching, the result was just too nice to pass up. During my last class of the day (Algebra II, so not a class relevant to this problem), a student wondered what would happen if we made a particular change to the problem statement. We discussed why it would likely break the result, but his question caused me to wonder out loud what would happen if we used the common internal tangents instead of the external ones.

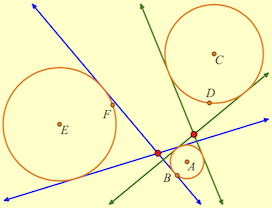
I might not have wondered at all had the student not done so first. And busy as that time of year is, I probably would have let it go anyway, but about a half hour after school the student and I passed in the hall and he asked if I had yet checked for any new results.

At that, of course, I could not let it go, though it would have been better yet if I’d been in a position to ask him to work on it himself. I played around with it that night and found the internal-tangent extension to Monge’s Theorem. Curiosity then impelled me to extend my sketch to consider cases in which some tangent pairs were internal and some were external. (My result is shown in this sketch, but I encourage you to try it yourself before downloading.)

When I showed students the result the next day, many found it fascinating, and gratifying because they had a sense that this result of their class discussion belonged to them collectively—not just to the student who had first raised a question and pressed the investigation. I told the students that I had done a quick search of the web and had found no reference to the extension. (I also observed that we should not assume that our result was new, as it might just not have been thought important enough for comment.) As we emphasize in class, however, discovery is always important personally, no less so for lacking priority. Whether one is the first is irrelevant to a discovery’s main value, which is to the discoverer.

The experience seemed a nice example of what is possible when we can help students develop habits of curiosity and of asking questions to probe new possibilities. It was also an example of learning and discovery as a collective enterprise in which one learner’s thoughts spur another’s. Finally, it put me in the role of being a learner as well, with my own curiosity stimulated by that of my students.

This incident also showed, of course, how Sketchpad makes possible such self-initiated investigations. In light of all that, I passed along the story and sketch to Scott Steketee from KCP Technologies, whose work with Sketchpad seems committed to that vision of learning and who I thought would find it gratifying. Scott encouraged me to write this up as a post for their blog.

All of which leads into a second story about collaboration, but that’s a story for another day.