David Henderson, the author of Experiencing Geometry, died this past December. I wrote about David in a prior post, and in particular, his approach of asking us to grapple with a small number of rich problems, allowing us to find our own, often non-traditional, ways of solving them over weeks at a time. In this post, I’d like to share one of David’s problems that he posed to us in Math 408 in 1991. It’s a lovely question, and one that I have not seen elsewhere.
Start with a quadrilateral ABCD. Create a scaled copy A’B’C’D’ so that when A’B’ is placed onto side CD of the original quadrilateral, the two sides match up (see below). Repeat this process over and over again, scaling each new quadrilateral by the same amount and attaching it the growing spiral of similar quadrilaterals. Then start over, repeating the same process to build a spiral onto side AC of the original quadrilateral using a scale factor of AC/BD.
Assuming that DC < AB and AC < BD, the two spirals converge in a point. Can you prove it? I recommend placing the double spiral on the complex plane and representing the transformations of quadrilateral ABCD in terms of complex number arithmetic (If you need a hint or would like to see how others approached the problem, read the blog feedback below and James Tanton’s two proofs, one and two).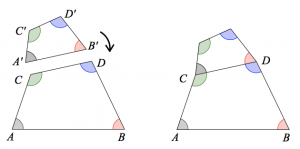
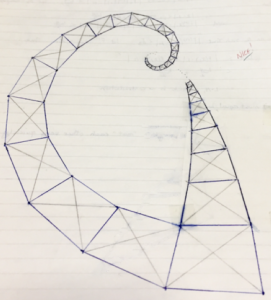
In 1991, we did not have dynamic geometry software that could easily build such a construction, so David asked us to cut out a quadrilateral and use it to draw as much of the two spirals as we could. Below is my illustration. Can you figure out how I might have used my paper quadrilateral to create the spirals?
Now, 27 years later, I’m able to not only construct the spirals easily and accurately with Sketchpad, but I can also drag the vertices of ABCD to watch the spirals react dynamically. Try it below (or here) with the Web Sketchpad model.
If you are interested in reading more about David, I recommend this Cornell Chronicle obituary. And this Flickr account shows pictures of David taken throughout his life.
I’ll close with a quote from David’s course syllabus:
JULY 2019 UPDATE: David’s double-spiral construction has been quite a hit! Suzanne von Oy extended the spiral pattern with Desmos, @jagarikin created two animations of the spirals (one and two), and this spiral from Vincent Pantaloni features Spiderman!
Thank you for posting this!
The fact that two spirals converge to a common point is a quick exercise in abstract nonsense: call the original points $C_0$ and $D_0$, and let $C_n$ and $D_n$ denote the images of $C_0$ and $D_0$ after $n$ iterations. Each time we iterate, the distance between $C_n$ and $C_{n+1}$ is scaled by the same quantity. In particular, $d(C_{n+1},C_{n}) = \alpha d(C_{n},C_{n-1}) = \alpha^n d(C_0, A)$, where $\alpha = d(C_0,D_0)/d(A,B) < 1$. Since $0 < \alpha < 1$, we have $\lim_{n\to\infty} \alpha_n = 0$, which means that the $C_n$ converge to a single point. A similar argument shows that the $D_n$ converge to a single point, and the fact that $d(C_n,D_n) = \alpha^n d(C_0,D_0)$ tells us that the two sequences converge to the same point.
Now… the actual point to which they converge is a little trickier. However, thinking of these guys as points in the complex plane with $A$ at the origin and $B$ on the positive real axis, then $C_1$ is given by (I think)
$$C_1 = C_0 + \alpha \underbrace{\left( \frac{C_0}{|C_0|} \cdot \frac{D_0 – C_0}{|D_0 – C_0|}\right)}_{=:\mathrm{e}^{i\theta}}. $$
Breaking this down, $C_0$ is the original point, as a complex number. We are going to add to this point (in the sense of addition in the complex plane) a point that looks like $C_0$ after a scaling by $\alpha$ (with $\alpha$ as above) and a rotation. The rotated, scaled point is $\alpha \mathrm{e}^{i\theta}$, where the angle $\theta$ is a little harder to work out: $C_0 / |C_0| = \mathrm{e}^{i \varphi_1}$, where $\varphi_1$ is the measure of the angle $\angle BAC_0$; while $(D_0-C_0) / |D_0-C_0| = \mathrm{e}^{i\varphi_2}$ is the measure of the angle $\angle EC_0D_0$, where $E$ is a point on the line parallel to $AB$ through $C_0$. Simplifying a bit,
$$ C_1 = C_0 + \alpha \mathrm{e}^{i\theta} . $$
Then $C_2$ is $C_1$ plus the point $C_0$ after two scalings and rotations. Hence
$$ C_2 = C1 + \alpha^2 \mathrm{e}^{2i\theta} = C_0 + \alpha \mathrm{e}^{i\theta} + \alpha^2 \mathrm{e}^{2i\theta}. $$
More generally,
$$ C_{n} = C_0 + \sum_{k=1}^{n} \left( \alpha \mathrm{e}^{in\theta} \right), $$
which is a convergent geometric series, and can be computed using the usual tricks.
I think.
Also, here's hoping that the TeX all works… :\
Oh, dear. The TeX seems not to work. Drat…
Let me also say (since I didn’t say this above), this is a lovely little problem. I like it quite a lot.
What a funny and lovely fact! Thanks for sharing.
My approach (using the lettering you used in the interactive model):
Put B at the origin of the complex plane. Then, to follow the spiral to the right, you compute RightLimit = D + D z + D z² + …, where z is the complex number representing the scaling and rotation of the quadrilateral into the quadrilateral to its right.
z = (A – D) / (C – B) = (A – D) / C
so
RightLimit
= D + D z + D z² + …
= D / (1 – z)
= D / (1 – (A – D) / C)
= C D / (C – A + D).
But this expression is symmetric – it stays the same when you flip C & D – so this is also what you get when you calculate UpwardsLimit.
Quick & rough QED!
Nice proof!
Here’s a version in Desmos Geometry that uses a geometric interpretation of the proof above to find the fixed point automatically: https://www.desmos.com/geometry/jfzsscdg8n
It first uses a translation to find (C+D-A), then define B to be 0 and (C+D-A) to be 1 to define a complex plane, and used a scaled rotation to multiply C by D in that plane to place the limit point, and then apply scaled rotations around that limit point to create the spiral transformations to apply repeatedly to the quadrilateral.
Wow, I didn’t think Desmos Geometry in its current state would be suitable for the construction.
Hi, here is a proof with no calculations :
Let $r$ and $s$ be the two similarities generating the spirals. Since their ratios are stricly smaller than one, they have fixed points $x_r$ and $x_s$, which are respectively their only fixed points. The fact that the iterations under $r$ and $s$ make everything converge to $x_r$ or $x_s$ is quite standard.
Now, it is quite easy to see (but less to write) that $r$ and $s$ commute (just look at what happens to the original quadrilateral after $rs$ and $sr$).
So we have $s(x_r) = s(r(x_r))= r(s(x_r))$ so $s(x_r)$ is a fixed point of $r$, so $s(x_r) = x_r$, because it is the unique fixed point of $r$. Finally, $x_r = x_s$ because it is the only fixed point of $s$.