Mirek Majewski was born in Poland and studied mathematics at the Nicholas Copernicus University in Poland with an M.S. and Ph.D. in non-classical geometries. He is a professor of mathematics and computer science at several universities – PNG University of Technology, Inter-University of Macau (now Saint Joseph University), Zayed University in United Arab Emirates, and New York Institute of Technology. He is the author of numerous articles and books on computer graphics, applications of computers in education, and the geometry of art and architecture. Some of his recent works are related to the geometry of Islamic art and the history of medieval Islamic mathematics. His book ‘Islamic Geometric Ornament in Istanbul’ provides detailed geometric constructions of many Islamic ornaments that can be seen in Istanbul. His new series of books, ‘Sketches on Geometry and Art,’ is a systematic overview of various geometric ideas embedded in ancient as well as modern architecture and art.  The most recent book in this series is a detailed review of geometric constructions that are essential for Islamic geometric ornaments designers. You can learn more about his work at http://symmetrica.wordpress.com/ and http://majewski.wordpress.com/.

–Guest post by Mirek Majewski

In this blog post, I will show how the mosaic in the entrance to the Sultan Ahmed Mosque in Istanbul can be created using tiles in the shape of regular hexagons with the help of Sketchpad. I will then show how you can embellish the mosaic by varying the patterns, shapes, and colors on the tiles.

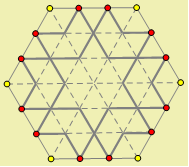
The mosaic contains zig-zag paths of double lines. Between them are formed regular hexagons and regular six-pointed stars. The picture below shows the pattern.It is easy to draw the outlines of large regular hexagons onto this pattern

The above illustration suggests a very natural way to design the pattern. We start with a regular hexagon, divide each side into thirds, and draw a grid connecting the trisection points. With this grid, we can easily build the Sultan Ahmed mosaic pattern. The Geometer’s Sketchpad construction is shown below.

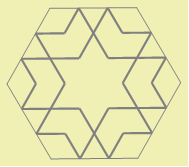
After removing all unnecessary elements of this construction we get a nice tile.

With this tile complete, we can save it as a reusable tool for easily constructing additional copies of the tile (See the interactive Web Sketchpad model at the end of this post.)

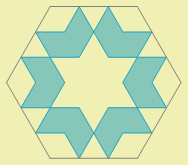
Using a bit of imagination, you can modify and colorize the tile. Here is an example.

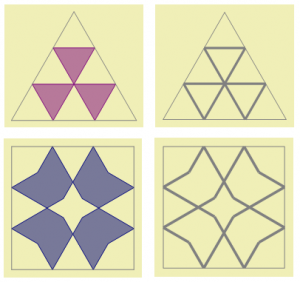
You can create many other patterns on the hexagonal tile using the grid from above. However, you should bear in mind that the paths on one tile should lead into the paths on adjacent tiles without any breaks and bends. This means a path passing through the edges should be straight. Of course all tiles should have the same size.

To add even more variety to our patterns, we observe that hexagonal tiles can be arranged so that there are triangular gaps between them. Thus we can create a triangular tile that will fit these gapes to match the hexagonal tiles surrounding it.

We can also construct square tiles to match the hexagonal and triangular tiles. Here are some examples.

In order to match lines on the square with lines on a hexagon, they should form 30° angles with a line perpendicular to the point on the edge of a tile.

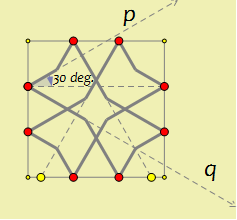
Starting from a hexagonal tile based on the mosaic in the Sultan Ahmed Mosque, we branched out into a set of three tiles – a hexagon, a triangle and a square. Your creativity will benefit significantly from this expanded choice of tiles. Using these three tiles, you can construct many interesting designs. Here is one of them:

And here is another pattern built with triangles and hexagons only.

Both patterns are regular tilings of the plane. In other words, they cover the plane without overlapping or gaps between tiles, and the pattern has a transitive symmetry in two different directions. How many regular patterns we can create with our tiles? What about less regular patterns? Can we produce them with this small set of tiles?

Below is a Web Sketchpad model for experimenting and building patterns of your own. The model comes with several tools, including a hexagonal tile tool based on the Sultan Ahmed mosque and two supplementary tile tools. Use the Link buttons to move from page to page.

The very last page of this geometric playground contains two red points. When you create your first tile, drag the two glowing points onto the red points to attach them. Continue by creating more tiles and attaching them to the ones in your sketch. If you’d like change the scale of your mosaic pattern or rotate it, just drag either of the two red points. If you wrongly place a tile or decide that you’d like to try something different, use the arrows above the tools to undo and redo each step of your work.