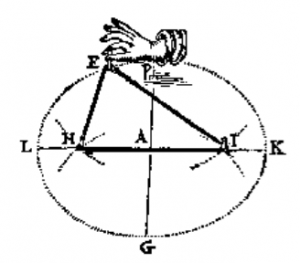
In a prior blog post, I described the pins-and-string approach to drawing an ellipse: Press two pins into a corkboard, place a loop of string around the pins, pull the string tight with a pencil, and trace the pencil tip’s path as you pull the pencil around the taut string. Guaranteeing that the traced path is an ellipse is this definition of an ellipse: An ellipse is the set of points P such that PF₁ + PF₂ is constant for two fixed points, F₁ and F₂.

You can see this method below in a picture from the 17th-century manuscript Sive de Organica Conicarum Sectionum in Plano Descriptione, Tractatus (A Treatise on Devices for Drawing Conic Sections) by the Dutch mathematician Frans van Schooten.

When I wrote about the pins-and-string construction, I provided a pre-built Web Sketchpad model of an ellipse based on this definition. Now it’s time for you to construct this model yourself using the tools I’ve provided in the websketch below. To get you started, I’ve included a short movie at the end of this post that walks you through the steps.

You’ll find this construction, as well as many others, in my book Exploring Conic Sections with The Geometer’s Sketchpad.