We live in a golden age of number puzzles. Sudoku is probably the most famous of all modern-day number puzzles, but there are many Japanese puzzles that are also gaining popularity, such as KenKen and Menseki Meiro. In this post, I’d like to introduce a number puzzle for young learners that predates these challenges by 40 years. Cross Number puzzles first appear in the 1960s Math Workshop curriculum written by Robert Wirtz, Morton Botel, and W. W. Sawyer. Below (and here on its own page) is a Web Sketchpad model containing four pages of cross number puzzles. (For this collection of puzzles, the numbers in the first column of the grid are multiples of 10, and the top two numbers in the second column are single digits.)

The cross number puzzle on page 1 contains five blank squares. To fill the squares with numbers, drag the red slider points. The square in the upper-right corner holds the sum of the two numbers in the top row, 50 +8. The square below it holds the sum of the two numbers in the second row, 30 + 8. Similarly, the squares at the bottom of the two columns contain the sum of the numbers above them (50 + 30 and 8 + 8). The number in the lower-right square can be described in numerous ways, including 50 + 8 + 30 + 8 or 50 + 30 + 8 + 8 or 58 + 38 or 80 + 16. In this manner, students encounter the commutative property for addition in a surprising, puzzle-based context long before they learn the concept formally.

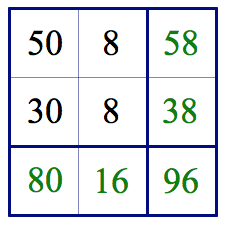
This is the first of 10 random puzzles on page 1, with each puzzle worth 10 points. If students solve a puzzle and press Next Puzzle, they’ll receive 10 points for a correct answer and 0 points for an incorrect answer. If they press Check Answer, the computer will tell them whether their solution is correct and allow them to fix any mistakes. However, each incorrect check deducts 2 points from the value of the puzzle. Pressing Play Another Round resets the score to 0 and allows students to play again with 10 fresh puzzles.

Pressing the arrow arrow key in the lower-right corner of the websketch moves to a fresh Cross Number challenge using the same rules, but with different squares left blank.

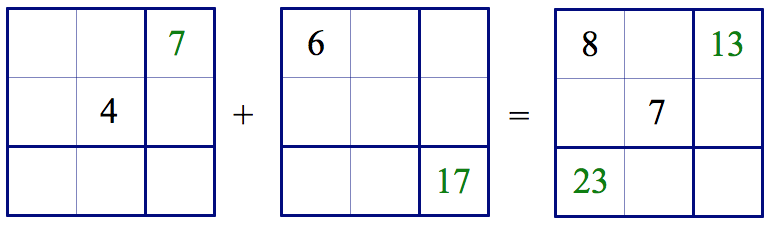
The Math Workshop curriculum features cross number puzzles across grade levels, taking the fundamental puzzle and embellishing it to deepen the mathematical explorations. On the left below, for example, are two cross number grids (with no restrictions about what numbers can appear where). On the right they have been added together. Can you determine the missing numbers?

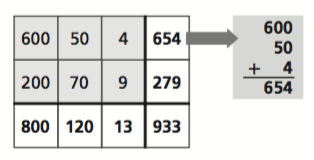
The recent ThinkMath! curriculum developed by Paul Goldenberg and his colleagues at EDC is based on Math Workshop, and makes liberal use of cross number puzzles. Below is an example from ThinkMath! that uses the cross number format to display 654 + 279 with partial sums:

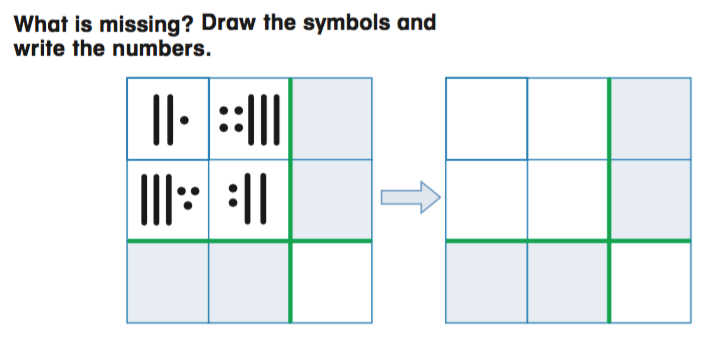
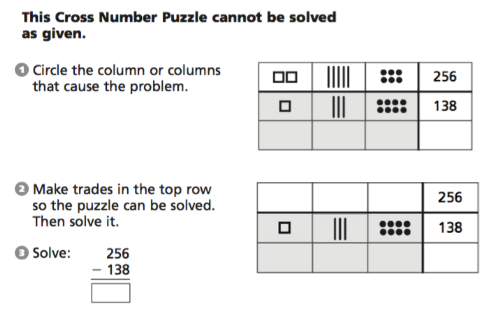
Here is another ThinkMath! example, using base-ten block notation (dots = 1, lines = 10, squares = 100) to model addition with regrouping.

And here is one more ThinkMath! example to model subtraction with regrouping. Subtraction puzzles are exactly like addition puzzles, but with the bottom row on the top.

In my next post, I’ll share a version of cross number puzzles suitable for beginning algebra students.

An annotated list of all our elementary-themed blog posts is here.