March 2023 UPDATE: If the dilation games below whet your appetite for challenges based on transformations, check out these Reflection and Rotation games as well.
What does dilation feel like?
I recently had the opportunity to work with a group of students who were testing activities that treat geometric transformations as functions (what I call geometric functions). I got lots of good ideas for improving the activities not only by watching the students, but also but also from their suggestions and the recommendations of their teacher, Jessica Shupik, and of my colleagues Daniel Scher and Mike Pflueger.
After several sessions of exploring reflections, translations, and rotations from a function perspective, we turned to the remaining transformation, dilations. The dilation activity emphasizes the way a function rule relates the independent variable (a point) and a dependent variable (its dilated image).
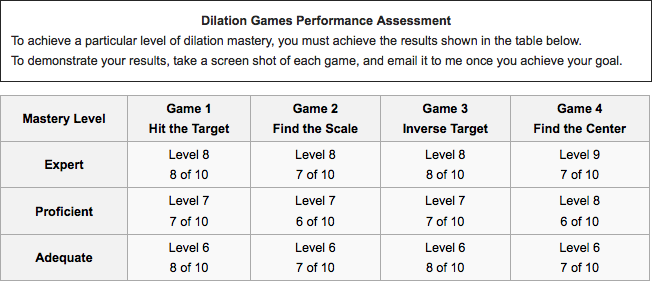
Ms. Shupik’s school promotes a mastery approach to grading and encourages performance-based assessments. With this in mind, we came up with three dilation games for assessing her students’ understanding:
- Game 1: Given an independent variable (a point) and a function rule (a center and scale factor), find the dependent variable (the dilated point).
- Game 2: Given the independent and dependent variables and the center point, find the scale factor.
- Game 3: Given the dependent variable and the function rule (the center and scale factor), find the independent variable. This third game is not solvable in the general case, but fortunately the dilate function has an inverse.
I later added Game 4: Given both independent and dependent variables and the scale factor, find the center of dilation.
Below (and here) is the Web Sketchpad model containing all four games. Use the page navigation controls in the lower-right corner to move between games.
(Note the labeling of the points, which is explained in the activity that precedes the assessment. The independent variable is x, to ease the later transition to algebraic functions, and the dependent variable is DC,s(x), using meaningful function notation as an abbreviation to indicate that this variable is “the dilation about C by scale factor s of x.” In the text at the top of the game pages, the full name is used, though the point itself is labeled in shorthand: D(x) for “the dilation of x.“)
As students progress through the levels of each game, the problems become harder and the hints become fewer, ramping up the challenge bit by bit. (To move from one level to the next, first press Reset to start a new game, and then drag the Level slider.)
Ms. Shupik set a level of achievement for each game, and told students to email her a screenshot when they met that level. In retrospect, it might be even more motivating to students to set a hierarchy of levels of mastery, perhaps something like this:
I was surprised while creating and testing this game to discover how much fun I had playing its higher levels. Without the security of measurements and numbers, I had to develop a feel for dilation, a sense for what a dilation by 7/4, or by –0.625, feels like.
The nice thing about this assessment, from my point of view, is that the students were learning about dilation, getting (like me) an experience-based understanding of it, even as they were trying to achieve a particular level of mastery. The assessment and learning occurred simultaneously.
I do not have enough time to go to level 8, I am still at level 1, although I have scored 32/32, but at Level 1 :-(. Please send me eMail message to which eMail address to send “screenshot” to prove this. Thanks in advance. Nenad
Hello Nenad, you ask a good question: how do you go from one level to the next? The answer is that you decide what level to use at the beginning of every game, and you can start a new game either by pressing the Reset button, or by refreshing your browser window. I set it up this way to make it easy for one teacher to tell her students “Keep practicing until you score 8 of 10 at Level 5” and for a different teacher to tell her students “You must score 15 of 20 at Level 8.” That way anyone can practice easier levels first, but for no longer than necessary; as soon as you know how to do Level 1, you can go to a higher level, and you can even skip levels if you like.
I have edited the original post to try to make this clearer.
Thanks for your comment,
–Scott