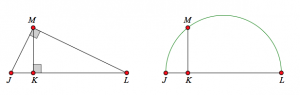
The picture below on the left shows a right triangle JML with altitude KM. This altitude is defined as the geometric mean of JK and KL. Using similar triangles, you can prove that JK × KL = KM². Another way to think about this construction is shown below on the right. Start with segments JK and KL placed end to end. Find the midpoint of JL and use it to construct a circle or semicircle with JL as its diameter. Construct a line through point K perpendicular to JL and mark where it intersects the semicircle at point M. Again, KM is the geometric mean of JK and KL since ∠JML (inscribed in a semicircle) is 90 degrees.
In Beautiful Geometry by Eli Maor and Eugen Jost, the authors use the geometric mean construction as a way to construct a square with area equal to a given rectangle. Using the semicircle construction of the geometric mean, they build a rectangle with side lengths JK and KL and a square with side length KM. Below is a picture from Beautiful Geometry showing the construction for several particular lengths.

When I saw the picture, I rushed to create a dynamic Web Sketchpad version of it. Below (and here on its own page), you’ll see my model. Press Animate to set the model in motion.
My interest in this problem dates back to 1990 when I was a graduate student in mathematics education at Cornell University taking a geometry course from David Henderson. David’s teaching philosophy was based on the Moore method, named after the topologist Robert Lee Moore. David gave us a small number of geometry problems and encouraged us to work on them for weeks at a time, letting us wrestle with the mathematics to gradually find our own, often non-traditional, ways of proving results. David’s geometry course became a textbook, Experiencing Geometry, co-written with Daina Taimina. One of the problems we explored in David’s class was finding a way to not only build a square with the same area as a rectangle, but to dissect and rearrange the pieces of the rectangle to become the square. Let’s look at some of the approaches we developed .
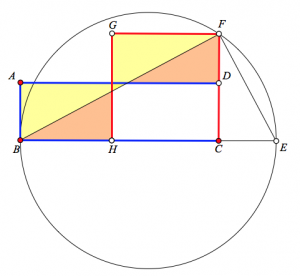
The construction below for dissecting rectangle ABCD into square GHCF is essentially the same as the Beautiful Geometry model, with AB = CE, except that the square has been flipped to the left and the rectangle flipped up so that the two quadrilaterals overlap. Using the color-coding as help, can you explain how to dissect the rectangle into the square? To prove your result, you’ll need to explain why the yellow triangles are congruent as well as the orange triangles. Click the arrow in the lower-right corner of the websketch above to move to its second page, where you can experiment with an interactive version of this construction.
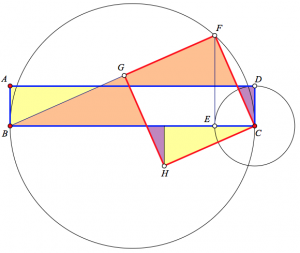
Below is another construction for dissecting rectangle ABCD into square GHCF. Starting with rectangle ABCD, construct a circle with BC as its diameter. Construct a second circle with CD as its radius and mark point E where the circle intersects BC. Construct a line perpendicular to BC that passes through point E. Mark point F where this line intersects the first circle. Construct a square with side FC. As before, can you explain and justify using triangle congruence how to dissect the rectangle into the square? Page 3 of the websketch displays an interactive version of the construction.
When I first saw this dissection method, I puzzled for a while trying to figure out how someone might have devised it. It looked very similar to the geometric mean approach, but not the same. It then occurred to me that I could use similar triangles BFC and FEC to prove that BC × EC = FC². And since EC = CD, that means the area of the rectangle is equal to the area of the square.
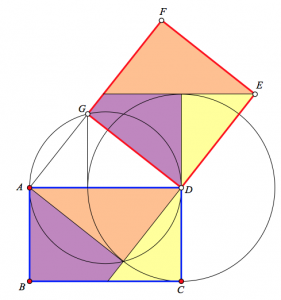
Finally, here is another dissection technique, similar to the one above, obtained by reflecting both the square and the rectangle so they do not overlap. It was discovered by Nashat Sobhee Ahmed and Donald Campbell, students of David Dennis at the University of Texas in El Paso. You’ll find an interactive version of this construction on the fourth page of the websketch.
You can build any of these dissection constructions on page 5 of the websketch using the collection of tools that come with the websketch.
Finding ways to dissect rectangles into squares is fascinating in its own right, but with these techniques in hand, you can apply them in service of a larger goal: Devising a method for dissecting an arbitrary polygon, such as the one below, into a square. First, cut the polygon into triangles. Then dissect each triangle into a parallelogram. Continue by dissecting the parallelograms into rectangles, and each rectangle into a square. For each pair of squares, use a Pythagorean Theorem dissection approach to combine the two squares into just one. Continuing this process with the squares, you’ll eventually be left with just a single square whose area is equal to the original arbitrary polygon. Pretty neat!
