Writing Mathematics with Sketchpad

In a recent blog post, Karen Coe referred to Conrad Wolfram’s opinion that programming is to mathematics what composition is to English. I’ve taught programming and written a lot of Sketchpad code, and I appreciate Wolfram’s analogy. In English class, students read books, poems, short stories, essays, and articles—but to gain a deep appreciation for literature , they must write as well. By composing their own stories, poems, and essays, students come to appreciate the beauty of a well-crafted sentence, the emotional impact of alliteration, the convincing nature of a closely-reasoned argument.

Wolfram is on the right track—to deeply understand and appreciate mathematics, students should not only read mathematics, but write it as well. Mathematics should be to them more than received wisdom; it should be a creative process. Creativity was a major objective when I taught AP Computer Science. I wanted students to take pride in the logical process of doing a project, and joy in having created something new and useful and even beautiful.

Recursive Logo program and sample output (see note below)

Programming is an excellent vehicle for mathematical activities. It’s profoundly logical in nature, resting on a well-defined set of rules and the combining of elements in carefully thought-out ways to build up more and more complex structures on the way to a finished program. It has explicit built-in support for conceptual abstraction (procedures and functions) and mathematical iteration (while and for loops as well as recursive procedures). The Logo program here, for instance, uses a recursive procedure called inspi to define the on-screen path of an imaginary turtle.

But programming isn’t available—or of interest—to many of our students. A few students (predominantly boys) take to it enthusiastically, but others find it too solitary, too impersonal, or too difficult, and most students have neither inclination nor opportunity to undertake interesting and satisfying projects. Even as I agreed with Wolfram’s analogy, I couldn’t help but think of another analogy that is, I think, both more accessible to students and more closely related to their math class: Dynamic geometry construction is to mathematics as composition is to English.

With Sketchpad, as with a word processor, students can start with a blank screen and combine the software’s basic objects to assemble, manipulate, review, share, and revise a complex creation. They can write their own mathematical compositions. Although the visual nature of Sketchpad makes it feel very different from a programming language, it is similarly logical, and it too provides mechanisms for conceptual abstraction (custom tools) and for mathematical iteration (the Iterate command). As the movie here shows, it’s not hard to use the Iterate command to rewrite the above Logo program in Sketchpad.

As in this example, students can write a Sketchpad short story about geometric shapes. They can set the stage by constructing and transforming a segment, elaborate using mathematical iteration, and develop characters and plot by changing the initial parameters and increasing the number of repetitions. They can bring the story to a climax by making and testing conjectures, and share their finished work using Hot Text and Action Buttons.

The Logo program implemented in Sketchpad, with a description,
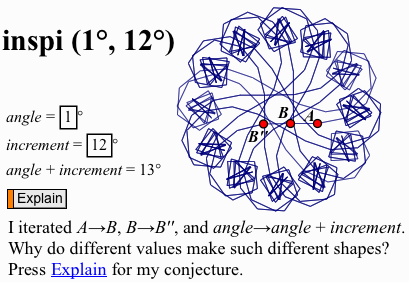
input parameters (1, 12), and resulting output

This is not the way teachers are used to teaching, nor the way students are used to learning. It is challenging for both—students’ initial mathematical writings will contain the equivalents of spelling errors and ungrammatical constructions, and teachers will struggle as they support student inquiry. English teachers are undeterred by such problems; so should we be as math teachers. If we help our students learn to write mathematics more creatively, who among us can imagine all the topics they will write about, the originality they will bring to their writing, and the compositions they will produce?

If you are new to Sketchpad, you might take a first step of learning to use the software to develop your own mathematical writing skills.  All of the Getting Started Tutorials, and many of the activities in the Sketchpad curriculum modules, begin with blank screens and include step-by-step instructions. As our English colleagues can tell us, such guided composition exercises provide useful scaffolding to help students build the skills and confidence to become creative writers of mathematics.

Or if you’re already familiar with Sketchpad, take this challenge: Write your own Sketchpad construction to do the same mathematics as the Logo program shown in the first image. If you need scaffolding, download this pdf with step-by-step instructions. The heart of the challenge comes when the construction is done—try a variety of input values and observe the resulting shapes. Continue your investigation and analysis until you understand and can explain how the input values determine the shape. Be sure to check your conjecture by predicting shapes for various inputs and testing those predictions.

2016 UPDATE: You can now explore this activity in Web Sketchpad, using a pre-built model.

Note: The Logo program referenced above is adapted from Al Cuoco, Paul Goldenberg, and June Mark: “Habits of Mind: An Organizing Principle for Mathematics Curriculum” (Journal of Mathematical Behavior 15(4):375-402, December, 1996).