In his 1947 book, One, Two, Three…Infinity, physicist George Gamow poses a pirate treasure problem that has since become a classic. Below is my reworded statement of the puzzle.
Among a pirate’s belongings you find the following note:
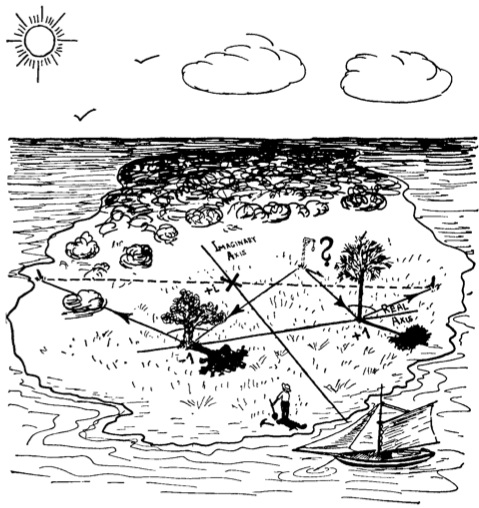
The island where I buried my treasure contains a single palm tree. Find the tree. From the palm tree, walk directly to the eagle-shaped rock. Count your paces as you walk. Turn a quarter-circle to the right, and walk the same number of paces. When you reach the end, put a stick in the ground. Return to the palm tree, and walk directly to the owl-shaped rock, again counting your paces. Turn a quarter-circle to the left, and walk the same number of paces. Put another stick in the ground. Connect the sticks with a rope and dig beneath its midpoint to find my treasure.
If the two rocks remain but the palm tree has long since died, can the riches still be unearthed?
Below (and here) is a dynamic Web Sketchpad model of the situation with point P representing the palm tree, points E and O the eagle and owl rocks, points S1 and S2 the sticks, and point T the treasure. Note that wherever you drag point P, the treasure stays in place. You can also create this websketch starting from scratch using the three tools (Segment, Midpoint, and Rotate) that accompany the model. Go to page 2 of the websketch (tapping the arrow in the lower-right corner) and watch the short movie at the end of this post for a quick tutorial.
Gamow’s solution to this problem makes lovely use of complex numbers. While I liked Gamow’s proof, I found myself wondering whether geometry alone would suffice to solve the problem. My Mathematics Teacher article describes my geometric solution. In this blog post, however, I’d like to share two geometric proofs created by David Lewine, a former teacher at the Young Women’s Leadership School in East Harlem, NY.
David’s proofs are really clever, and both owe their discovery to his investigations with Sketchpad. For each of the two proofs below, use the arrows in the lower-right corner of the websketch to move from page to page.
For more information about the Pirate problem, be sure to check out Michael de Villiers’ resources as well as this article by Stavroula Patsiomitou. And because you can never have enough pirate problems, here’s one that requires hyperbolas to solve.
I put together a unit on proof for my geometry classes that culminated in this activity, based on your MT article. The rest was from Rethinking Proof with GSP. Man, I miss Key Curriculum.