Here is a wonderful geometry problem from Japan: The five triangles below are all isosceles. The quadrilaterals are all rhombi. The shaded quadrilateral is a square. What is the area of the square?
I wondered at first whether the English translation of the problem was correct because with so many side lengths unspecified, it was hard to believe that the square’s area could be uniquely determined. But the sheer strangeness of the problem led me to persist. And as with many geometry problems, I turned to Sketchpad to look for insights.
Building the isosceles triangles with the specified base lengths seemed laborious so I made the lengths adjustable. I also made one other significant change: rather than constructing rhombi (which led to a rather boring interactive model), I built parallelograms instead. This made for more interesting interactivity and did not change the essential elements of the solution.
With so many isosceles triangles and parallelograms in the construction, I decided to color-code the segments to make it easier to identify those that were equal in length. Below (and here on its own page) is a Web Sketchpad version of my work. Before reading further, try dragging points G, H, I, J, and K to make your own discoveries.
As I dragged the points, I looked for invariants—those elements of the construction that remained the same while others changed. I was initially surprised that dragging point H translated quadrilaterals SQTU, PMQS, and LHMP while keeping their side lengths and angles intact But as I thought about it, the behavior made sense once I accounted for all the dependencies in the construction. I can imagine a great class discussion that focuses on explaining what changes and does not change—and why—as each point is dragged.
One observation particularly relevant to the problem was that for SQTU to be a square, GB and KE needed to be of equal length. I also noted that for ∠SQT to be 90°, GB must be perpendicular to KE since these two segments are parallel to SQ and TQ, respectively. To view the length and angle measurements in the websketch above, press the Show Measurements button. You can then make SQTU a square by adjusting points B and G.
Given that the state of SQTU depended entirely on ΔABG and ΔEFK, I realized that I could collapse the construction into one that showed only the essential elements needed to solve the problem. In order, I dragged point C to B, point D to C, and point E to D, leaving the construction shown below. With all the extraneous elements of the construction gone, you should now be able to determine the area of the square.
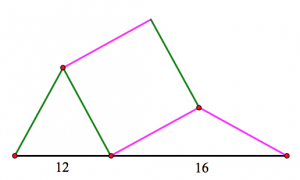
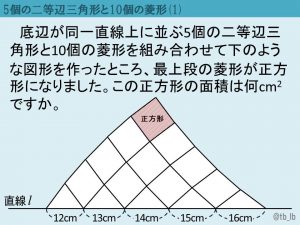
GeoGebra rhombus version of your lovely sketch: https://www.geogebra.org/m/TuXGZp7x
Thanks for sharing the problem – so much coolness to notice.
Nice to see your version of the model! I’m planning a follow-up post on this problem for next month.