Twitter is a great place to find geometry problems. The July 22, 2017 post of xylem presented the image below with two squares, ABCD and BFGE, sharing a vertex. Given that AE = 5, what is the length of DG?

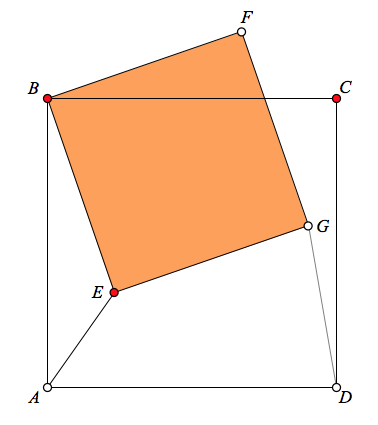
My first thought was that surely the problem was underspecified. Without knowing more about the size of ABCD and the orientation of BFGE, how could the length of DG be unique? Well, there was one way to check—I built myself a Web Sketchpad model! The model below (and here on its own page) allows you to drag point E, keeping length AE constant (The length of AE is controlled by the horizontal segment to the left of the squares.)

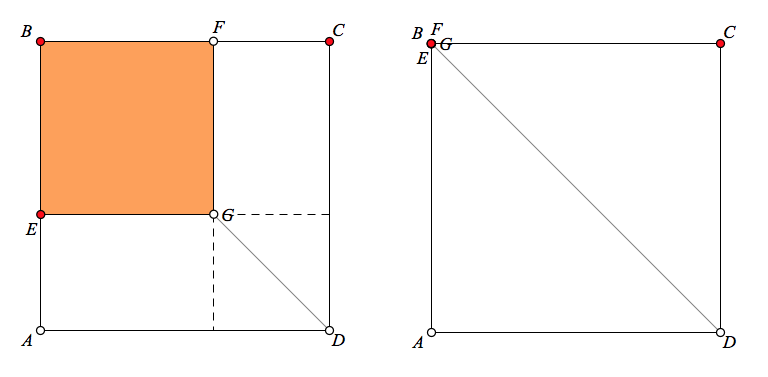
Sure enough, regardless of point E‘s location, DG‘s length remains invariant. Before jumping to a proof, we can determine DG‘s length by picking special locations for point E. In the picture below left, point E lies on AB. We can see from the added  dashed segments that GD is the diagonal of a square with side AE, so GD = 5√2. Another way to see the relationship between AE and DG is to drag point E onto AB and then zero-out square BFGE entirely by adjusting AE’s length until it equals AB (See the picture below right.)

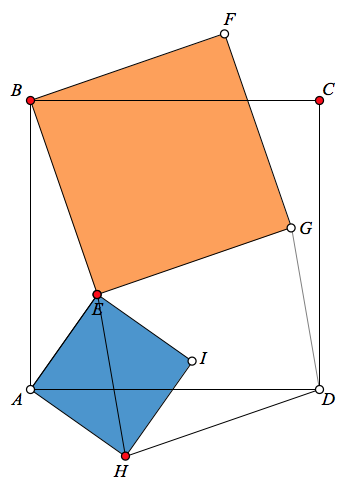
To show that GD = 5√2 regardless of point E‘s location, Twitter users   offered a number of proofs. Below (and on page 2 of the websketch), we create parallelogram AEGH. Can you prove that ΔGHD is an isosceles right triangle?

As a second proof, the illustration below (and page 3 of the websketch) shows a blue square erected on AE. Can you prove that EH = GD?

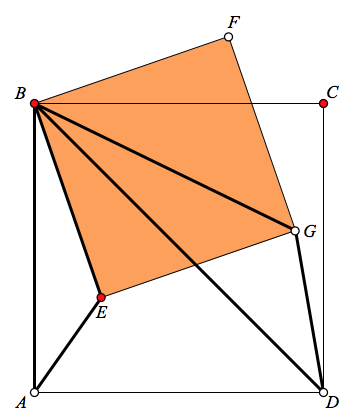
Finally, one of the shortest proposed proofs requires only that you show ΔGBD∼ΔEBA with scale factor √2. I’ll leave the details to you.

The arrangement of the two squares in this problem reminded me of an area-based proof of the Law of Cosines first described to me by David Dennis. In the picture below (and on page 4 of the websketch), there are three squares and two congruent parallelograms. By sliding ΔBFC down onto  ΔAHD and sliding  ΔCID across onto  ΔBEA, we can see that the sum of the areas of the orange square, the blue square, and the two parallelograms is equal to the area of square ABCD. The Law of Cosines activity from the Sketchpad module Pythagoras Plugged In by Dan Bennett challenges you to add the algebraic steps needed to show the connection to the familiar Law of Cosines statement. And as a bonus, if you drag point E so that ∠BEA = 90°, you create a geometric dissection proof of the Pythagorean Theorem.

If you flip through the various page of the websketch above, you’ll see that page 5 is left blank. You can use this page to create any of the interactive models from page 1-4 using the four tools that come with the websketch as well as our new format palette. The how-to movie below will get you started.