A recent post on an NCTM discussion group asked about tools to help students visualize and understand addition and subtraction of integers. We wanted to make a visualization tool for students that they could use in multiple ways. The result is the Web Sketchpad model below (and here).  Page one focuses on addition while page two displays a subtraction model. (Worksheets and teacher notes are here.)

Drag the two circles to represent an addition or subtraction problem and then press the numbered buttons (or use the Present All button to show the animated steps one after the other.) Without resetting, drag the circles to observe how the model changes as you change the problem.

An important objective of this pair of models is to encourage students to develop a single consistent number-line visualization for both addition and subtraction, and to realize that there’s only one difference between the two models: to subtract you just negate (flip) the second number and then add it.

Importantly, the animation never actually displays the answer; this visualization is designed to emphasize the process, and the student must determine the answer herself by inspecting the model.

When using this or any similar model, it can be very useful to require students to draw the model first, before writing down the answer to the problem.

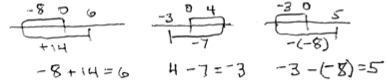
The physical act of drawing is an aid in helping students to understand and remember the connection between the model and the answer. By omitting the ticks and labels on the number line, the drawing helps students strip non-essential elements of the model and develop a robust abstract understanding.

You’ll know your students have “gotten it” when they can look at a problem, “see” the two operands appear on an imaginary number line, and immediately write down the sum or difference.

April 2025 Update: For a related model that helps students visualize addition and subtraction, check out our new Sliding Rulers model.