I must admit that I am addicted to triangle shearing problems . I've written about them before, and will be revisiting them soon in my City College geometry class. I mention this because several weeks ago, I encountered a problem in the LinkedIn feed of mathematics educator Continue Reading ››
Category Archives: Geometry
Visualizing a Dynamic Triangle
Below is a problem taken from Dietmar Küchemann's Algebradabra site.

Many problems that mix geometry with algebra invariably shortchange the geometry. For example, the angles of a triangle might be labeled x, … Continue Reading ››
Rotation Designs
It’s a gripe I’ve shared before, but I’ll repeat it—the typical high school geometry approach to introducing transformations is boring. Fresh from learning the definition of a translation, reflection, rotation, or translation, students are whisked off to the safety of the coordinate plane and asked to explore the numerical effect of reflecting a … Continue Reading ››
Some Triangle Shearing Investigations
When I taught a geometry methods course at City College last fall, I devoted an entire class to investigating area. We focused on problems where triangles were sheared, transforming into new triangles, but maintaining their area. The two Web Sketchpad activities that follow introduce shearing and present a problem with a surprising result … Continue Reading ››
Maximizing Triangle Area
In the February 1954 issue of Mathematics Teacher, Paul C. Clifford describes an optimization problem from his trigonometry class. Of all isosceles triangles ABC with sides AB and BC of length 12, which one has the maximal area? Clifford told his class that an exact solution to the question required calculus. One student, … Continue Reading ››
Constructing Rectangles with Constant Perimeter and Constant Area
In the fall of 2023, I taught a geometry methods course at City College here in New York. While my goal was to make use of Web Sketchpad throughout the semester, I knew that the most effective use of the software required activities that coupled it with hands-on modeling. Two such opportunities arose … Continue Reading ››
Constructing Daisy Designs
With nothing but a compass, students can construct a lovely daisy design consisting of seven interlocking circles, all of the same size.
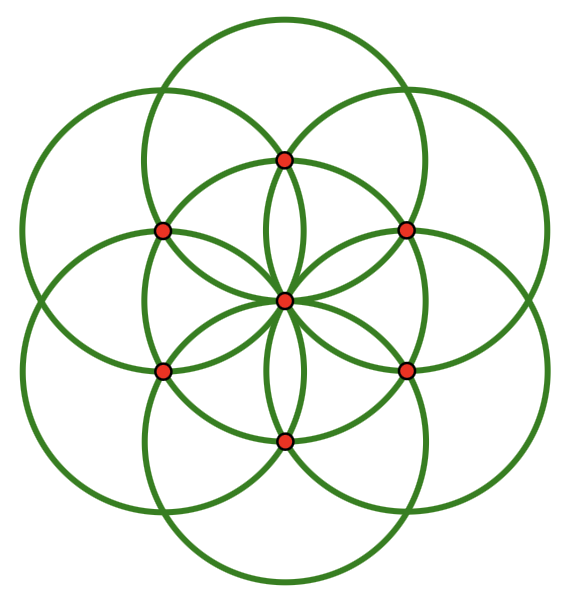
I was delighted to see that the U.S. postal service chose to feature … Continue Reading ››
The Mysteries of Polygon Flats
What do you get when you cross geometry with the classic murder mystery game Clue? Why, the Mysteries of Polygon Flats, of course!
In my prior post, I offered examples of how Web Sketchpad can help students classify special quadrilaterals like squares, rectangles, kites, parallelograms, … Continue Reading ››
Classifying Quadrilaterals
Ah geometry, how you suffer from a lack of attention in the elementary grades! Rare is the curriculum that doesn't stuff geometry into its final chapter, waiting patiently in line behind number and operation.
But the one geometry topic that does command attention is classifying two-dimensional shapes into … Continue Reading ››
Teaching with Web Sketchpad
This past semester, I taught a geometry course for teachers at City College here in New York. As you might expect, Sketchpad figured heavily in the course contents. But unlike other semesters when desktop Sketchpad was my tool of choice, this time, I took the plunge and limited myself to Web Sketchpad.