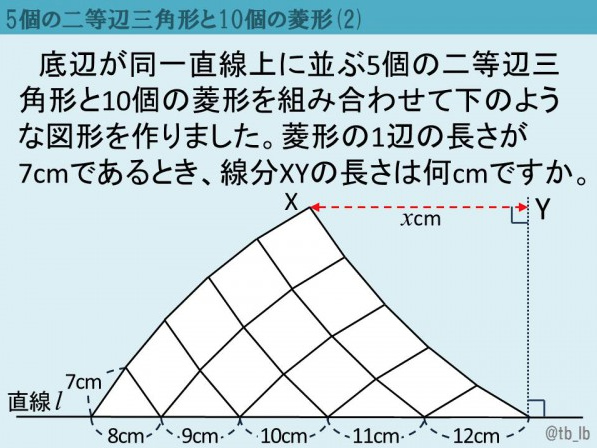
In my last post, I presented a lovely geometry problem from Japan that was ideally suited to a dynamic geometry approach. Below is a new problem whose construction is nearly identical to the original one. The text says, “Five isosceles triangles have their bases on one line, and there are 10 rhombi. One length of the rhombus is 7 cm. What is the length of XY?”

Based on my experience with the previous problem, I had a hunch that the problem statement could be altered to create a more generalized result. I ignored the specific values of all the lengths to create the interactive Web Sketchpad model below (and here on its own page), with 10 parallelograms rather than 10 rhombi. Even with these substantial changes, I was pleased to discover that no matter which of the red points I dragged, the length of XY remained invariant. Try it!

I hesitate to say any more about the problem without giving away its very satisfying solution. I will, however, point you to a simplified version of this model on page 2 of the websketch above (tap the arrow in its lower-right corner) that may be helpful.

And here is one more question to consider: How does the distance of point X from AB relate to the heights of the five isosceles triangles?