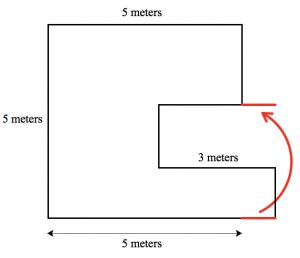
At a recent meeting of mathematics content coaches (many from the organization Reimagined) we investigated the following problem:  What is the perimeter of the polygon below?

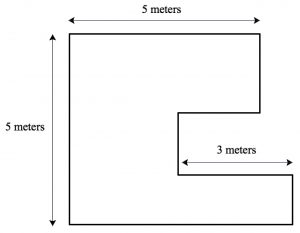
It appears at first that there isn’t enough information to solve the problem. Indeed, the lengths of only three of the polygon’s eight sides are provided. But as the coaches dug in, they recognized that the three unknown vertical lengths could be shifted to the left to align with the 5-meter segment. The availability of color markers made this idea easy for them  to visualize: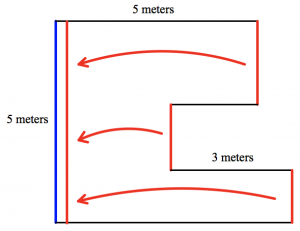

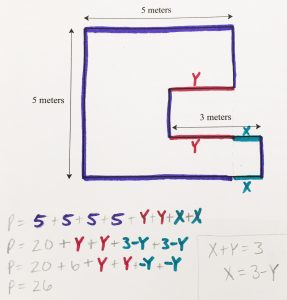
To determine the sum  of the polygon’s four horizontal sides, many of the coaches turned to algebra. Below is an example of how one coach assigned x’s and y’s to the polygon’s sides and was able to determine the perimeter:

There was certainly a big tug towards algebra when solving this problem, but it  does allow for purely geometric solutions as well. In the illustration below, the 5-meter and 3-meter lengths (displayed in red) are translated straight down. We see that taken together, the sum of the two red sides is equal to the sum of the two blue sides. Thus the sum of the polygon’s horizontal lengths is 16 meters.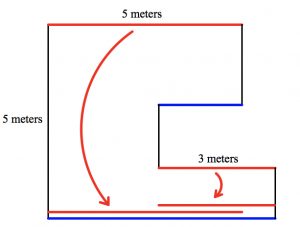

Another way to think geometrically about the situation is to divide the lower polygon side into a 5-meter length and an extra length shaded in red. By moving this red length up, we see that horizontal sides now all have known lengths: 5 + 3 + 3 + 5, moving from top to bottom.

As a more concrete approach, we can assign a length to segment AB below and use that information to determine the length of CD. For example, if AB = 1 meter, then CD = 7 meters. If AB = 1.5 meters, then CD = 6.5 meters. And if AB = 2 meters, then CD = 6 meters. In all three cases, the sum of AB and CD is 8 meters. While these numerical values in themselves don’t explain why the sum of lengths AB and CD should be constant, they do alert us to a mathematical pattern that we can then try to explain.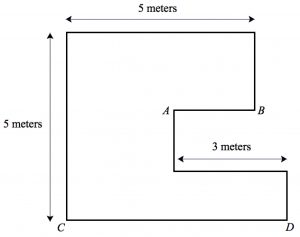

We can also examine the extreme cases. In the top illustration below, I’ve made the length of segment AB just a smidgen less than 3 meters, so for all intents and purposes, the four horizontal segments have lengths of 5, 3, 3, and 5. And in the bottom illustration, I’ve made the length of  AB nearly 0, so the lengths of the three remaining horizontal segments are 5, 3, and (nearly) 8.  In both extreme cases, the sum of the horizontal lengths is 16 meters.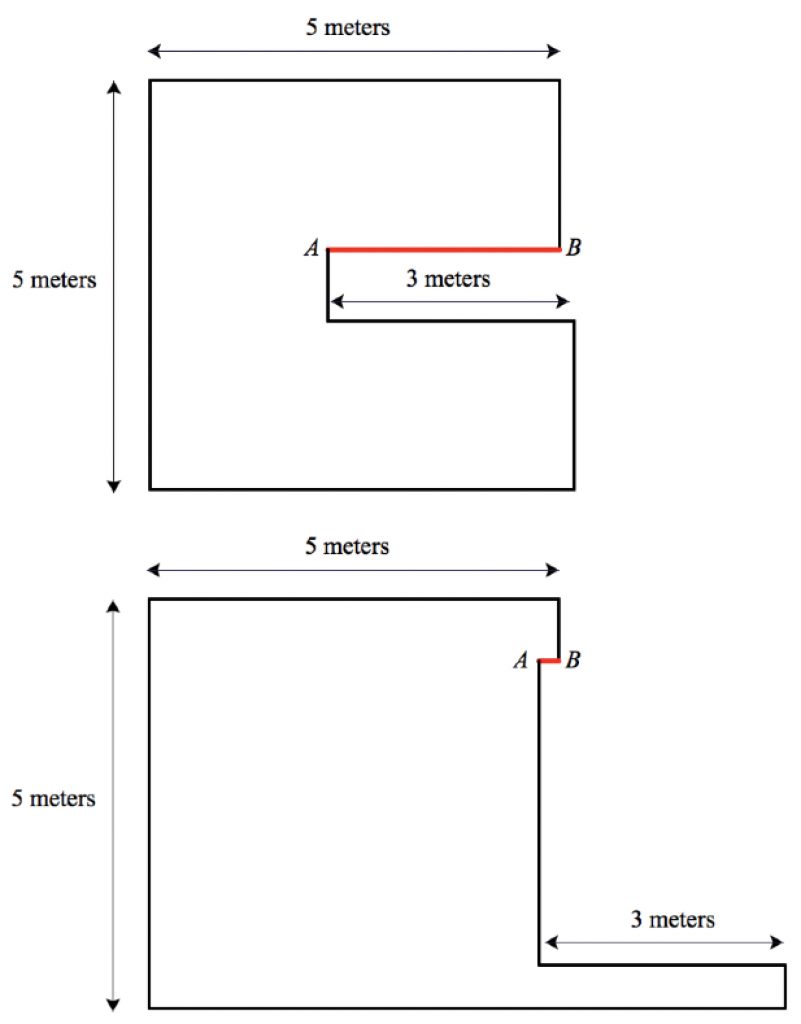

How do students in your class, whether it be third grade or high-school geometry, think about and solve this problem? Let us know!