 My first thought was that surely the problem was … Continue Reading ››
My first thought was that surely the problem was … Continue Reading ››A Geometry Gem from Twitter
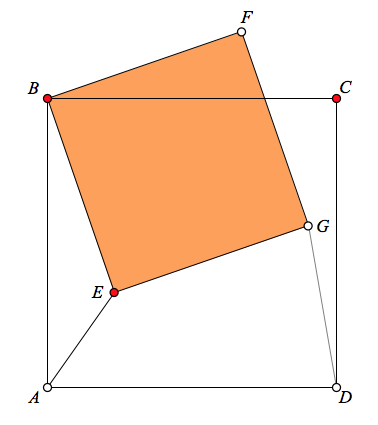
Twitter is a great place to find geometry problems. The July 22, 2017 post of xylem presented the image below with two squares, ABCD and BFGE, sharing a vertex. Given that AE = 5, what is the length of DG?  My first thought was that surely the problem was … Continue Reading ››
My first thought was that surely the problem was … Continue Reading ››
 My first thought was that surely the problem was … Continue Reading ››
My first thought was that surely the problem was … Continue Reading ››
 As interesting as many of the presentations have been, they've also been …
As interesting as many of the presentations have been, they've also been …