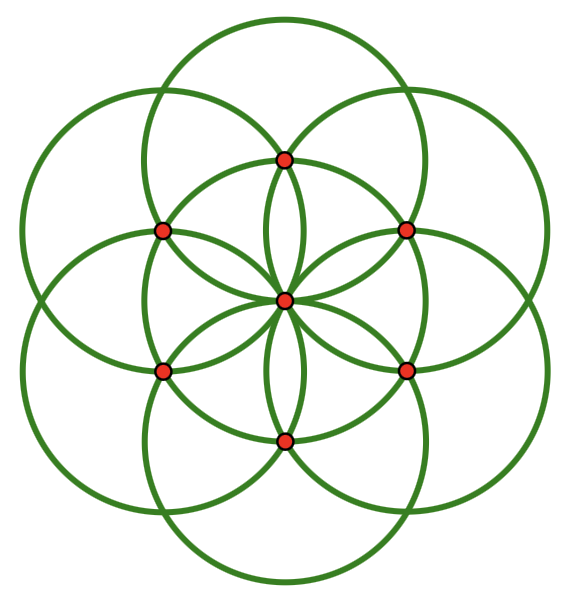
With nothing but a compass, students can construct a lovely daisy design consisting of seven interlocking circles, all of the same size.
I was delighted to see that the U.S. postal service chose to feature … Continue Reading ››
With nothing but a compass, students can construct a lovely daisy design consisting of seven interlocking circles, all of the same size.

I was delighted to see that the U.S. postal service chose to feature … Continue Reading ››
Eleven years ago, I wrote a post titled What is All the Fuss About Lines? In it, I discussed the difficulties that students encounter when asked to determine the equation of a line. Faced with formulas for calculating slope, the point-slope form of a line, and the slope-intercept form, students lose … Continue Reading ››
What do you get when you cross geometry with the classic murder mystery game Clue? Why, the Mysteries of Polygon Flats, of course!
In my prior post, I offered examples of how Web Sketchpad can help students classify special quadrilaterals like squares, rectangles, kites, parallelograms, … Continue Reading ››
Ah geometry, how you suffer from a lack of attention in the elementary grades! Rare is the curriculum that doesn't stuff geometry into its final chapter, waiting patiently in line behind number and operation.
But the one geometry topic that does command attention is classifying two-dimensional shapes into … Continue Reading ››
While most numbers lead anonymous lives away from the mathematical spotlight, eiπ occupies hallowed ground. Douglas Hofstadter writes that when he first saw the statement eiπ = −1, “. . . perhaps at age 12 or so, it seemed truly magical, almost other-worldly.”
At the risk of deflating the celebrity status of … Continue Reading ››
This past semester, I taught a geometry course for teachers at City College here in New York. As you might expect, Sketchpad figured heavily in the course contents. But unlike other semesters when desktop Sketchpad was my tool of choice, this time, I took the plunge and limited myself to Web Sketchpad.
This post, inspired by the work of Al Cuoco, uses Web Sketchpad to explore a transformations approach to complex numbers.
Given two segments and their midpoints, what quadrilaterals can you build using the segments as the diagonals of the quadrilateral?
This post examines the connections between origami and geometry in the context of a new book written by Daniel Scher and Marc Kirschenbaum.
This post presents virtual dances based on geometric transformations. As a penguin travels around a polygon, you, as a frog, must match its movements, but with the added challenge of dancing as a reflection, rotation, or dilation of the penguin’s path.